Current P through a certain non-metallic rod is given as i0=0.2V32 where V is potential difference across it. The rod is connected in series with a resistance to a 12 volt ideal bettery. What should be resistance ( in Ω) so that power dissipated in the resistance is twice that of rod.
The correct Answer is:5
To solve the problem, we need to find the resistance R such that the power dissipated in the resistance is twice that of the power dissipated in the non-metallic rod. Let's go through the steps systematically.
Step 1: Understand the given information
We are given that the current I0 through the rod is expressed as:
I0=0.2V3/2
where V is the potential difference across the rod. The rod is connected in series with a resistance R to a 12-volt ideal battery.
Step 2: Set up the equations for power
The total voltage from the battery is 12 volts. The voltage across the rod is V, and the voltage across the resistance R is 12−V.
The power dissipated in the rod Prod can be expressed as:
Prod=V⋅I0
The power dissipated in the resistance PR is given by:
PR=(12−V)⋅I0
Step 3: Set up the relationship between the powers
According to the problem, the power dissipated in the resistance is twice that of the rod:
PR=2Prod
Substituting the expressions for power:
(12−V)I0=2VI0
Step 4: Simplify the equation
Since I0 is common in both terms, we can cancel it out (assuming I0≠0):
12−V=2V
Rearranging gives:
12=3V
Thus,
V=123=4 volts
Step 5: Calculate the current I0
Now, substituting V=4 volts back into the expression for I0:
I0=0.2⋅(4)3/2
Calculating (4)3/2:
(4)3/2=(22)3/2=23=8
Thus,
I0=0.2⋅8=1.6 A
Step 6: Find the resistance R
Now we can find the resistance R using the power relationship:
PR=(12−V)I0=(12−4)⋅1.6=8⋅1.6=12.8 W
The power dissipated in the resistance can also be expressed as:
PR=I20R
Setting the two expressions for power equal gives:
I20R=12.8
Substituting I0=1.6:
(1.6)2R=12.8
Calculating (1.6)2:
(1.6)2=2.56
Thus,
2.56R=12.8
Solving for R:
R=12.82.56=5Ω
Final Answer
The required resistance R is:
5Ω
We are given that the current I0 through the rod is expressed as:
I0=0.2V3/2
where V is the potential difference across the rod. The rod is connected in series with a resistance R to a 12-volt ideal battery.
The total voltage from the battery is 12 volts. The voltage across the rod is V, and the voltage across the resistance R is 12−V.
Prod=V⋅I0
The power dissipated in the resistance PR is given by:
PR=(12−V)⋅I0
According to the problem, the power dissipated in the resistance is twice that of the rod:
PR=2Prod
Substituting the expressions for power:
(12−V)I0=2VI0
Since I0 is common in both terms, we can cancel it out (assuming I0≠0):
12−V=2V
Rearranging gives:
12=3V
Thus,
V=123=4 volts
Now, substituting V=4 volts back into the expression for I0:
I0=0.2⋅(4)3/2
Calculating (4)3/2:
(4)3/2=(22)3/2=23=8
Thus,
I0=0.2⋅8=1.6 A
Now we can find the resistance R using the power relationship:
PR=(12−V)I0=(12−4)⋅1.6=8⋅1.6=12.8 W
The power dissipated in the resistance can also be expressed as:
PR=I20R
Setting the two expressions for power equal gives:
I20R=12.8
Substituting I0=1.6:
(1.6)2R=12.8
Calculating (1.6)2:
(1.6)2=2.56
Thus,
2.56R=12.8
Solving for R:
R=12.82.56=5Ω
The required resistance R is:
5Ω
Similar Questions
The current I through a rod of a certain metallic oxide is given by I=0.2V1/2 , where V is the potential difference cross it. The rod is connected in series with a resistance to a 6 volt battery of negligible internal resistance. What value should the series resistance have so that :
A) the current in the circuit is 0.4 A
B) the power dissipated in the rod is twice that dissipated in the resistance.
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionThere identical point masses, each of mass 1 kg lie in the xy-plane at points (0, 0), (0, 0.2 m) and (0, 2m, 0). The net gravitational force on the mass at the origin is:
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View Solutionthe current developed in a real conductor is given I=aV1/2, where V is the potential difference acid the conductor. When it is connected with resistance of RΩ in series with a battery of 6 volt shown in the figure , the power developed in conductor is twice the power generated in resistance of RΩ . find the value of R.[a=0.2AVolt−1/2]
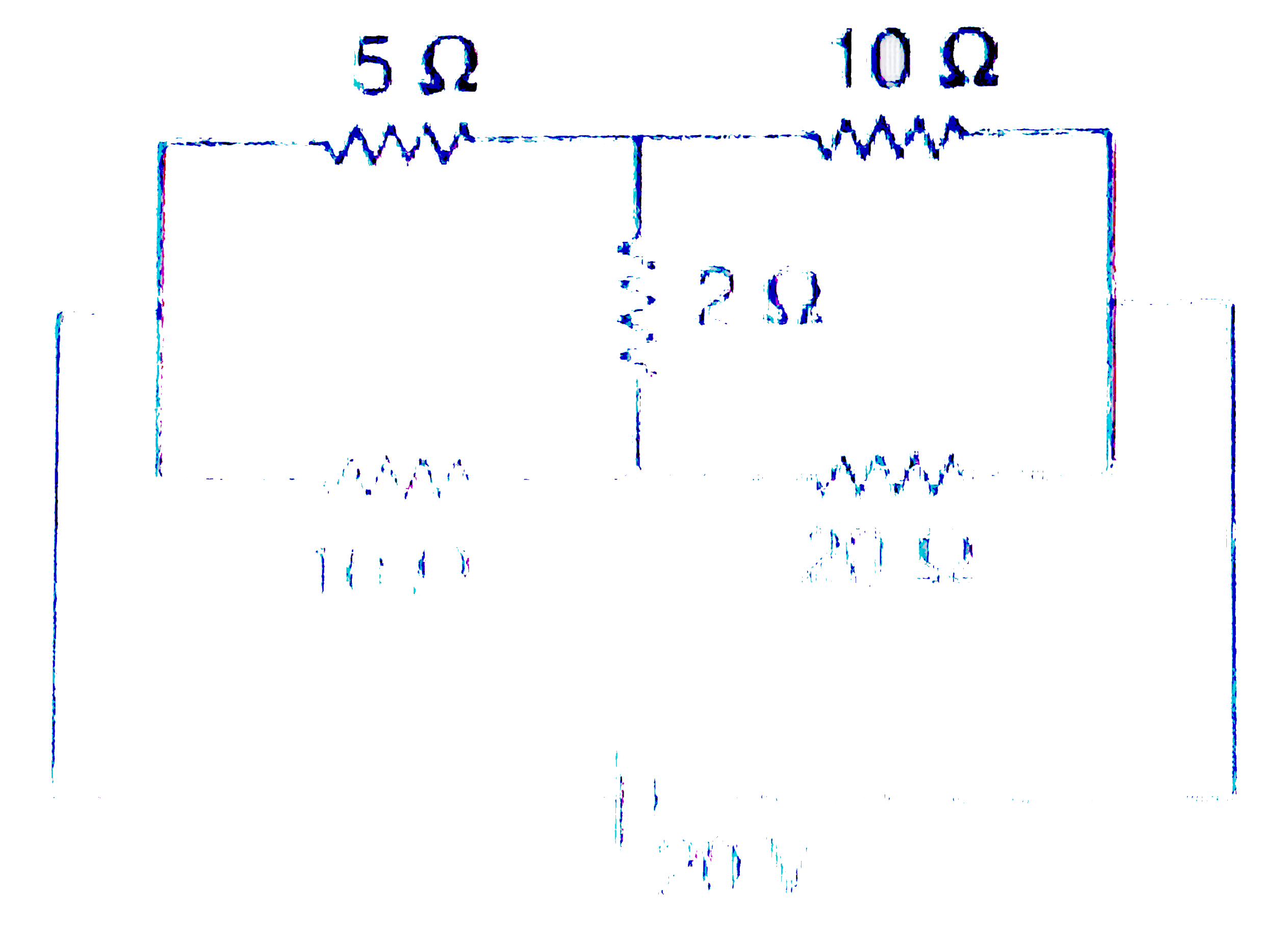
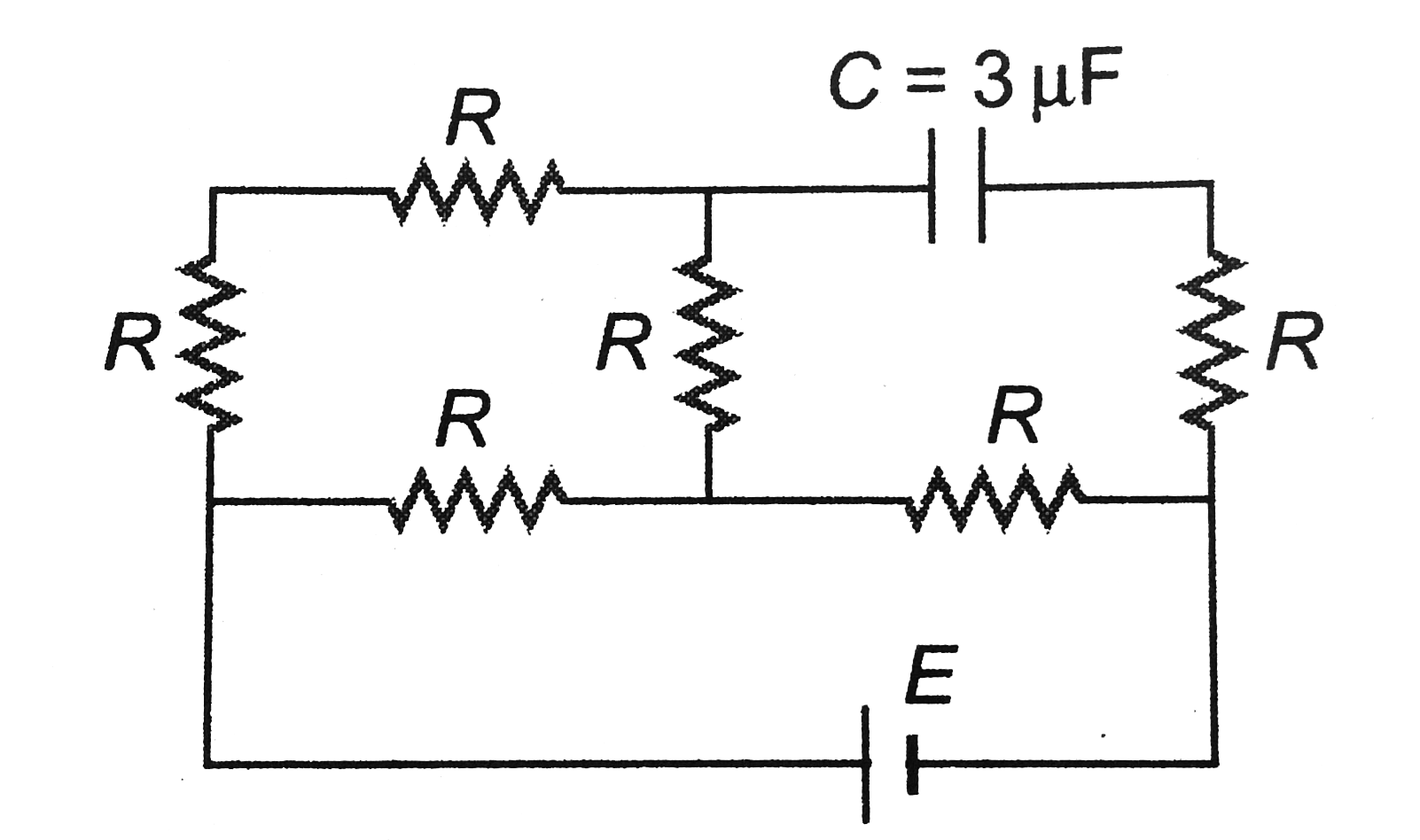
View SolutionIn the circuit the potential difference across the capacitor is 10V. Each resistance is of 3Ω The cell is ideal. The emf of the cell is
View SolutionCalculate the potential difference across the ends of a wire of resistance 2Ω'whenacurrentof1.5 A passes through it.
View SolutionA battery of 3.0 V is connected to a resistor dissipating 0.5 W of power . If the terminal voltage of the battery is 2.5 V , the power dissipated within the internal resistance is :
View SolutionA potentiometer wire 10 long has a resistance of 40Ω. It is connected in series with a resistances box and a 2 v storage cell. If the potential gradient along the wire is 0.01Vm the resistance unplugged in the box is
View SolutionThe potential difference between A and B is V. The values of some resistances are shown. The other resistance are equal in values. What should be the value of each of these resistances so that current in circuit is V/3R.

View Solution
