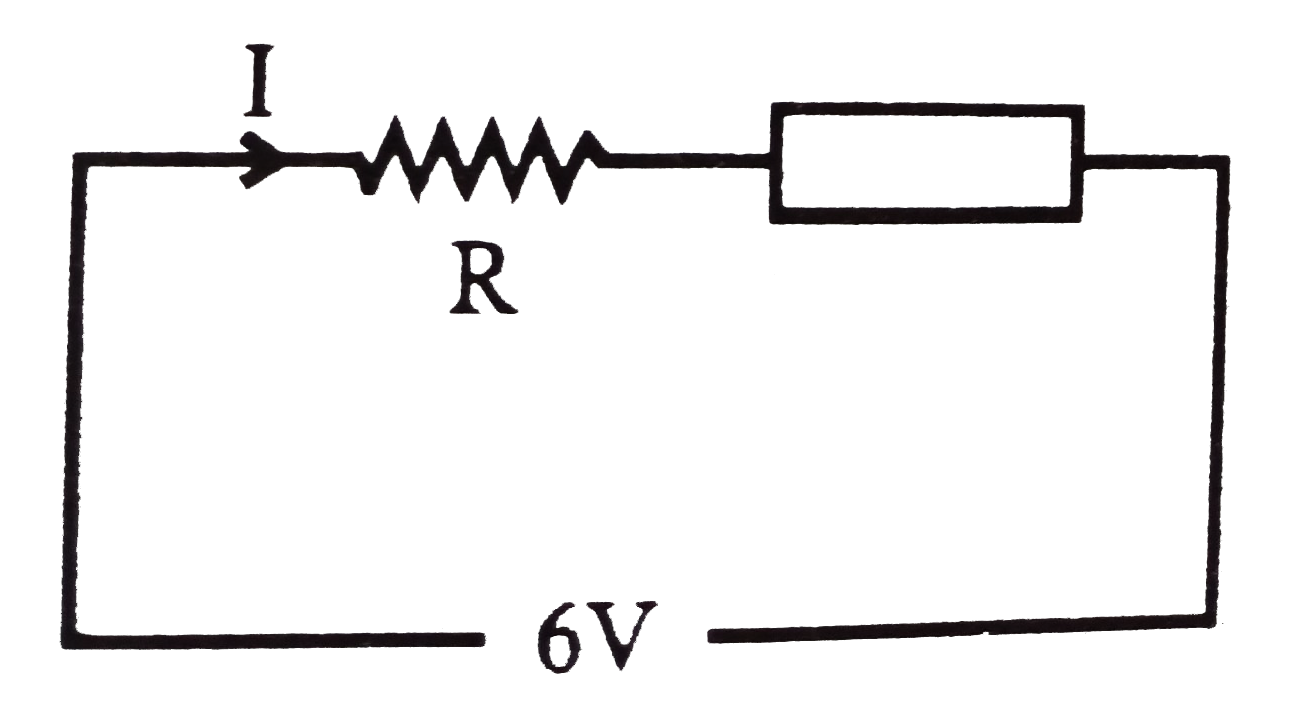
The current I through a rod of a certain metallic oxide is given by I=0.2V5/2, where V is the potential difference across it. The rod is connected in series with a resistance to a 6V battery of negligible internal resistance. What value should the series resistance have so that:
(i) the current in the circuit is 0.44
(ii) the power dissipated in the rod is twice that dissipated in the resistance.
The correct Answer is:(i)10.52Ω;(ii)0.3125Ω
(i) I=0.2V5/2⇒0.44=0.2V5/2
115=V5/2⇒12125=V5
V=1.37 volt
I=0.2V5/2
I=6−VR
0.44=6−1.37R⇒R=10.12Ω
(ii) 2I2R=VI⇒2IR=V....(1)
V=(6−IR)....(2)
From (1) and (2) V=4 volt
I=0.2V5/2=0.2(4)5/2=6.4
IR=2⇒6.4R=6
R=13.2=0.3125Ω
Similar Questions
A rod resistor obeys non-linear relationship between V and l-according to I=√V/10 This rod is connected in series with a resistance to a 20 V battery of practically no resistance. Find this series.resistance for the following cases
(a) the current in the circuit is 0.4 A.
(b) the power dissipated in the rod is twice that dissipated in the resistance
View SolutionCurrent P through a certain non-metallic rod is given as i0=0.2V32 where V is potential difference across it. The rod is connected in series with a resistance to a 12 volt ideal bettery. What should be resistance ( in Ω) so that power dissipated in the resistance is twice that of rod.
View Solution
Knowledge Check
A 3 volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be
 A1AB1.5AC2AD1/3A
A1AB1.5AC2AD1/3AA battery of e mf 10 V and internal resistance 3Ω is connected to a resistor as shown in the figure. If the current in the circuit is 0.5 A . then the resistance of the resistor will be
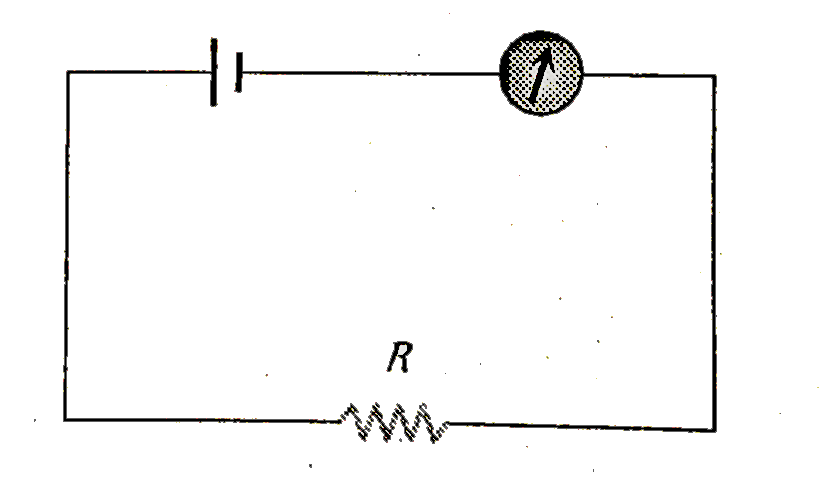 A19ΩB17ΩC10ΩD12Ω
A19ΩB17ΩC10ΩD12ΩA potentiometer wire has length 10 m and resistance 20Ω . A 2. 5 V battery of negligible internal resistance is connected across the wire with an 80Ω series resistance. The potential gradient on the wire will be
A5×10−5V/mmB2.5×10−4V/cmC0.62×10−4V/mmD1×10−5V/mm
A resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, find (i) the resistance of the resistor, (ii) the terminal voltage of the battery.
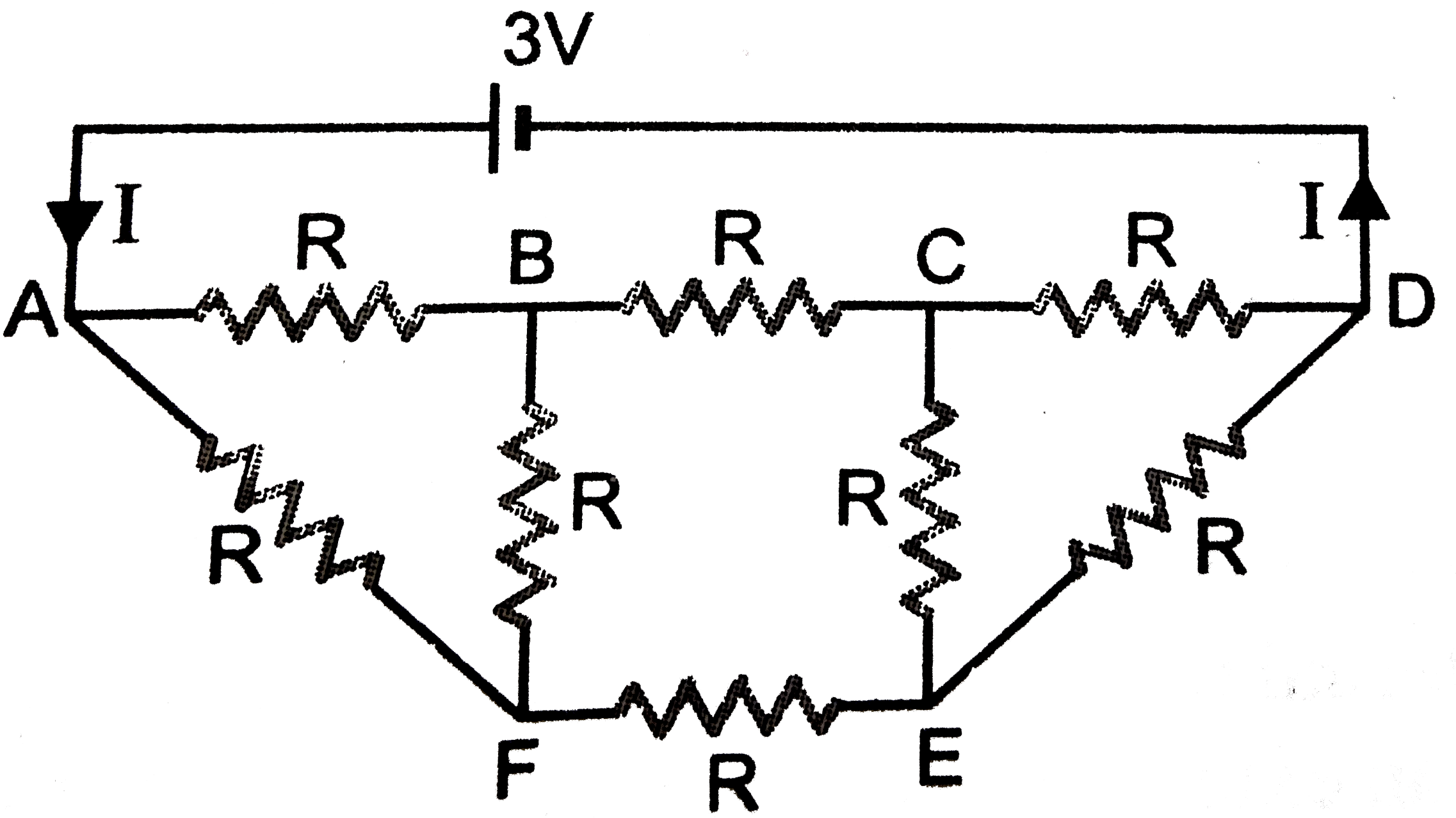
View SolutionShows a network of eight resistors battery of resistance R(=2Ω) connected in a 3V battery of negligible internal resistance. The current I in the circuit is
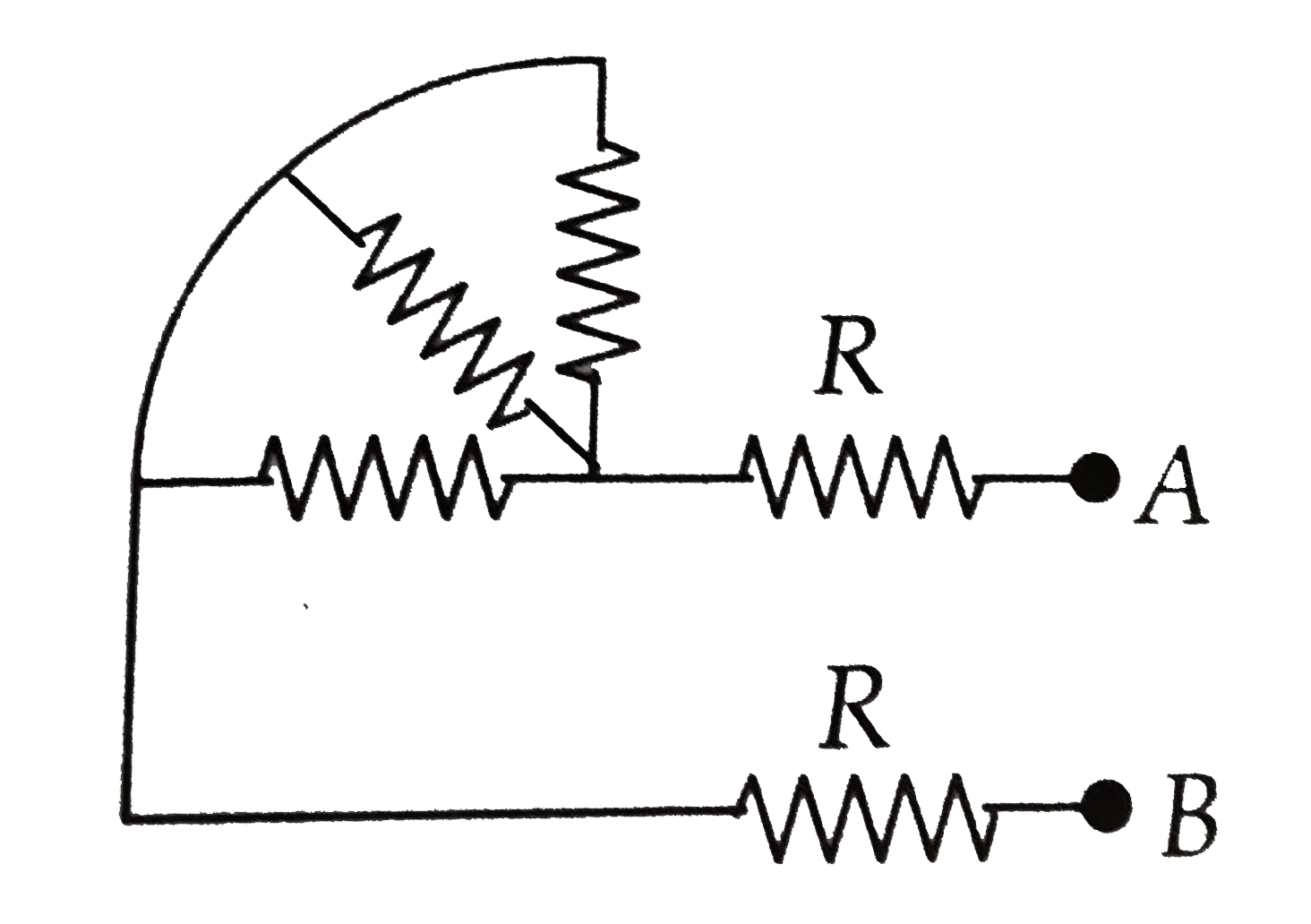
View SolutionThe potential difference between A and B is V. The values of some resistances are shown. The other resistance are equal in values. What should be the value of each of these resistances so that current in circuit is V/3R.
View Solution

