A small element l is cut from a ciruclar ring of radius a and λ charge per unit length. The net electric field at the centre of ring is
E=K(λ)dlR2 (towards −x)
E=K(λ)dlR2 (towards +x)
E=Kλdl2R2 (towards −x)
E=Kλdl2R2 (towards +x)
The correct Answer is:B
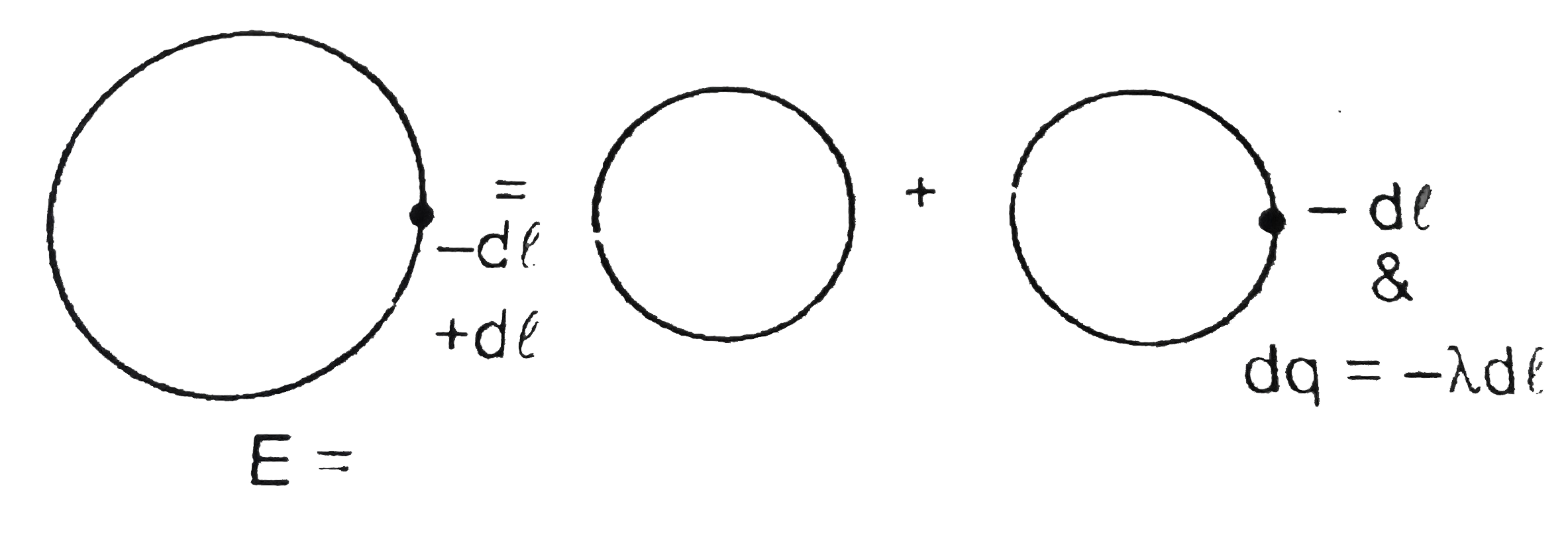
k(Q)R2=−KλdlR2
Similar Questions
A charged wire is bent in the form of a semicircular arc of radius a. If charge per unit length is λ coulomb/metre, the electric field at the centre O is
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is

View Solution
A small part of dl length is removed from a ring having charge per unit length λ. Find electric field at centre due to remaining ring.
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionThe linear charge density on upper half of semi-circular section of ring is λ and that at lower half is −λ. The direction of electric field at centre O of ring is :

View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
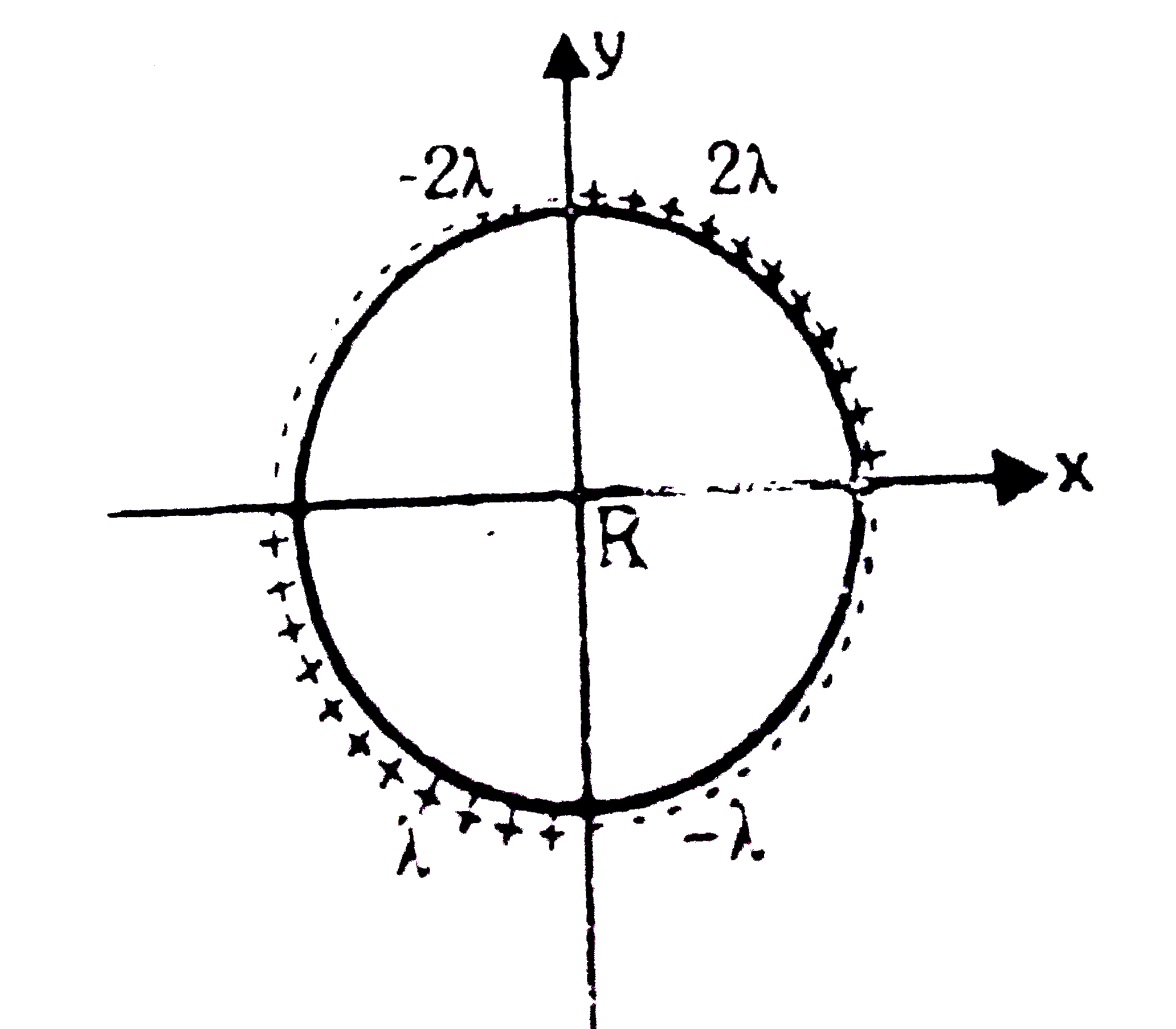
View SolutionThe charge per unit length of the four quadrant of the ring is 2λ,−2λ,λ and −λ respectively. The electric field at the centre is:
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View Solution
