A rod of length L can be hinged at varius points on it to work as a compound pendulum. At what distance from one end of the rod should be hinged so that there are only two point on the rod (each side of centre of mass) for which time period is same.
0.5 L
0.2 L
0.4 L
0.3 L
The correct Answer is:B
Time period will be minimum about a point at a distance K
(radius of gyration) from COM.
for rod k=L2√3≅0.29L on either side of COM
From on end 0.5l±0.29=0.21L,0.79L
≅0.2L,0.8L
Similar Questions
A rod of length L is suspended vertically from a point at a distance x from one end to oscillate under gravity. What should be x (approximately) so that it oscillates with minimum time period?
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
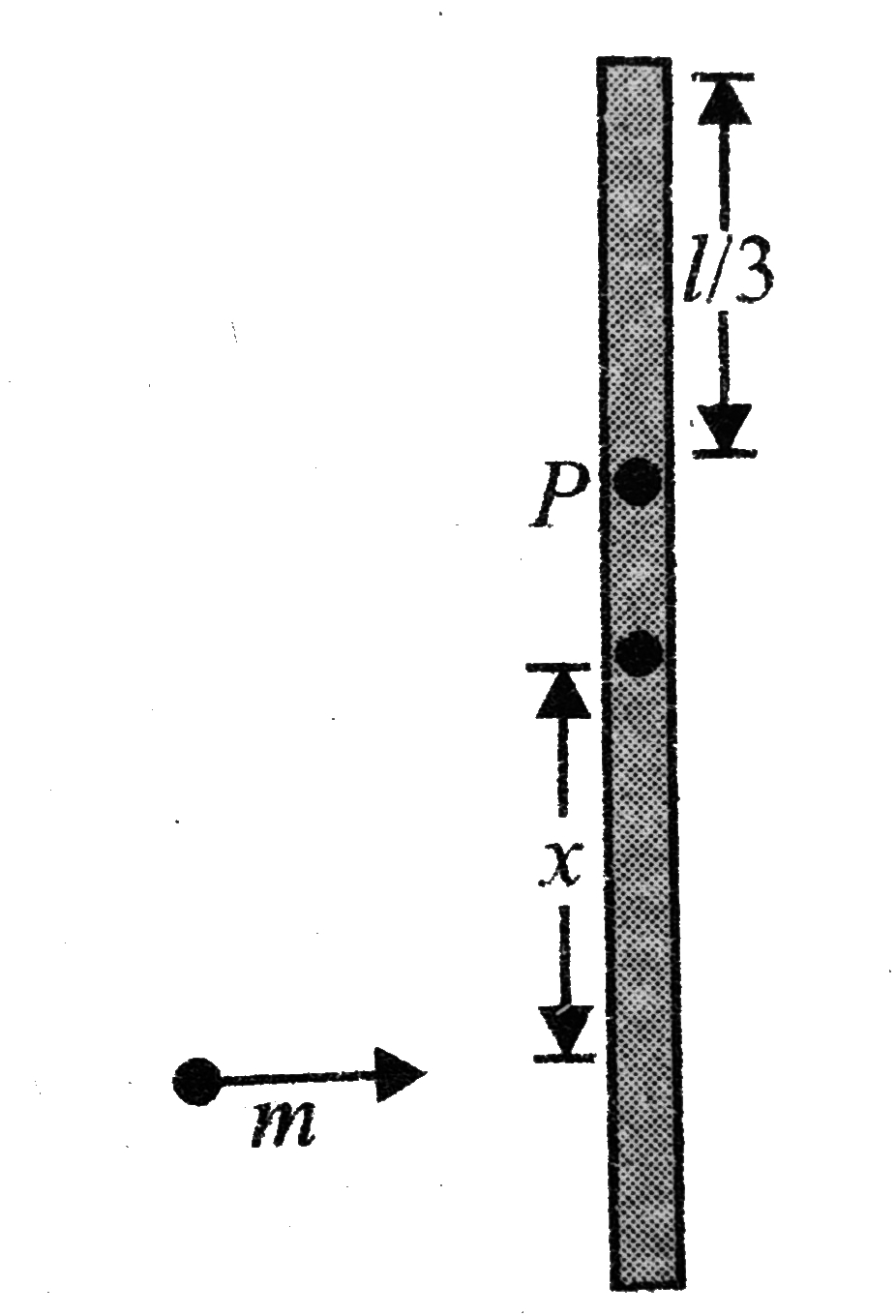
View SolutionCompound pendulum are made of A rod of length l suspended through a point located at distance l/4 from centre of rod. Find the time period in each case.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
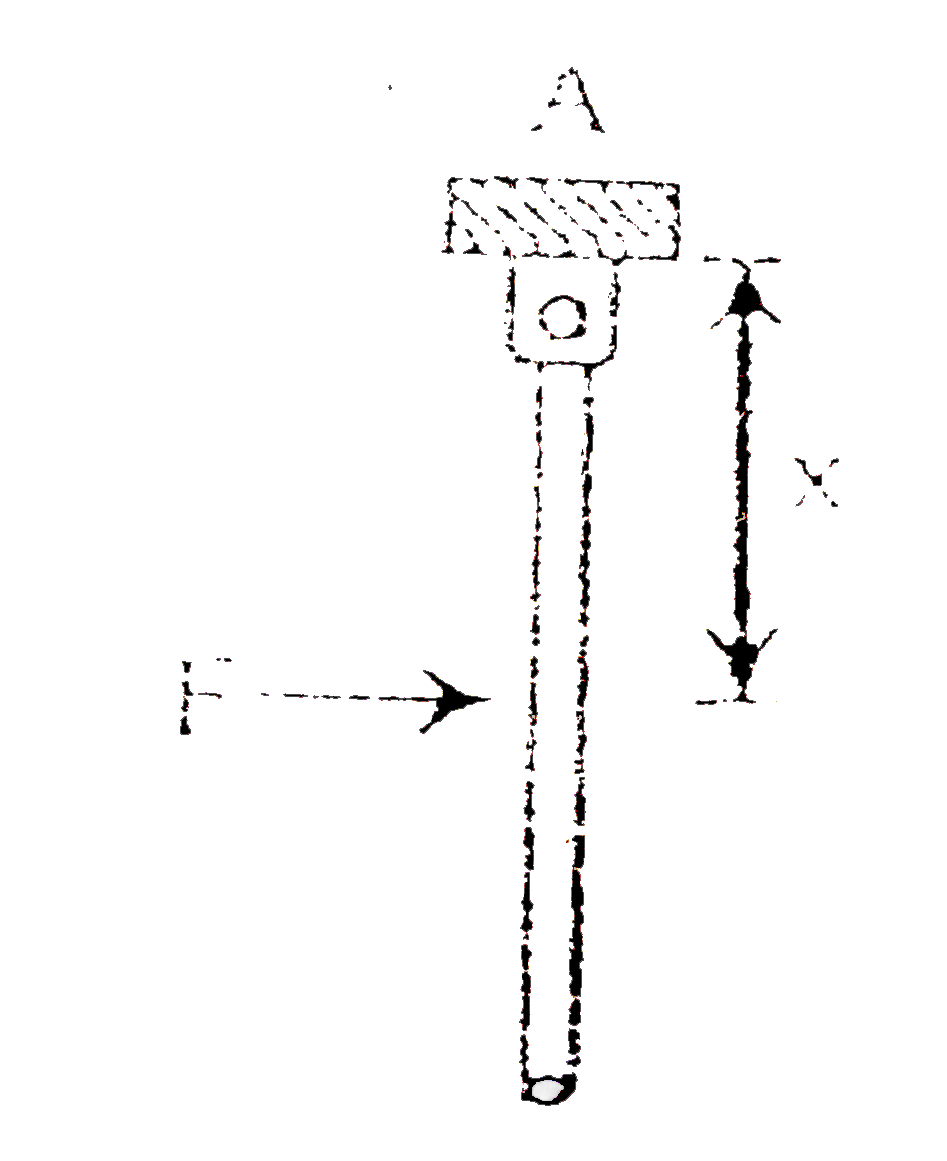
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
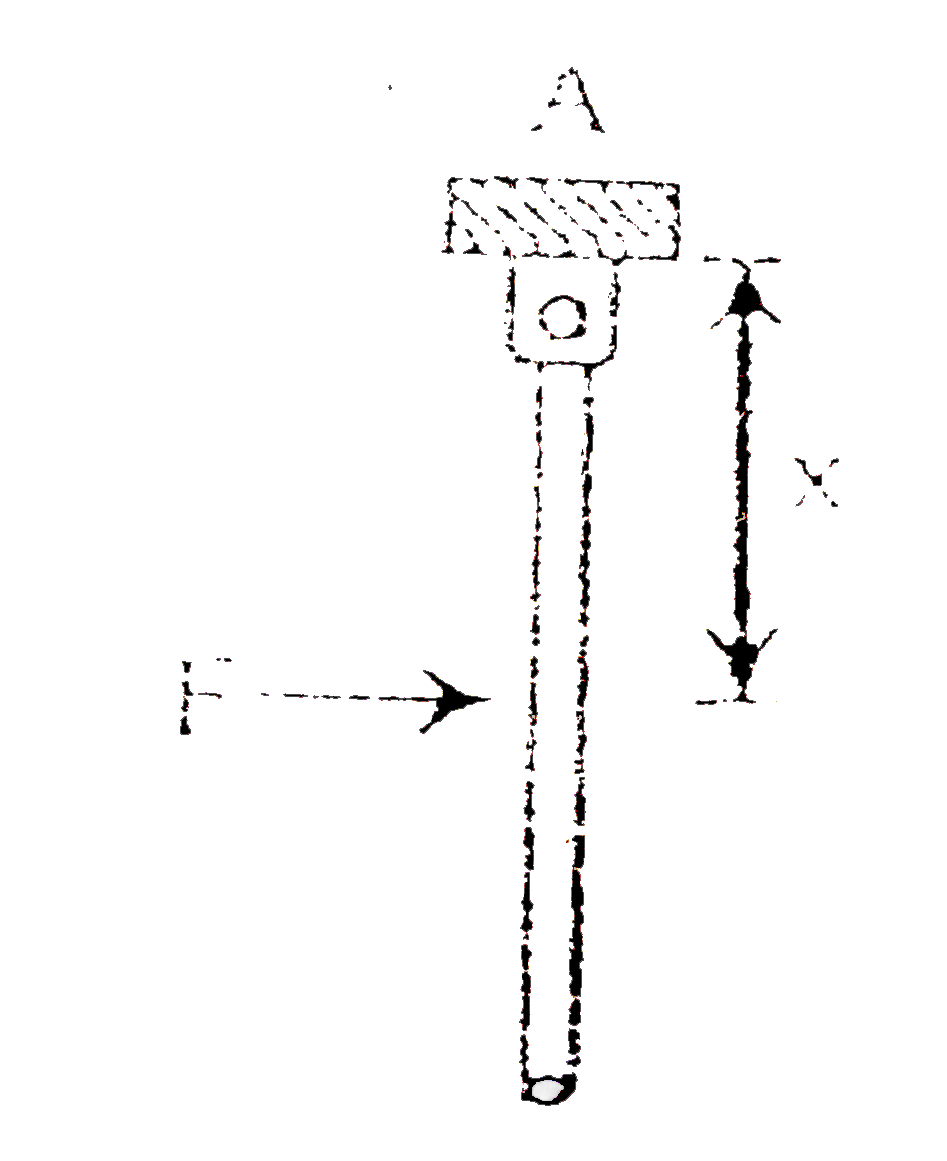
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View Solution
