A rod of length L is suspended vertically from a point at a distance x from one end to oscillate under gravity. What should be x (approximately) so that it oscillates with minimum time period?
L/12
L/3
5L/12
2L/3
The correct Answer is:C
To determine the distance x from one end of a rod of length L that minimizes the time period of oscillation when suspended vertically, we can follow these steps:
1. Identify the Center of Mass (CM):
The center of mass of a uniform rod of length L is located at a distance L2 from either end.
2. Define the Distance d:
If the rod is suspended at a distance x from one end, then the distance d from the center of mass to the pivot point is:
d=∣∣∣L2−x∣∣∣
3. Calculate the Moment of Inertia I:
The moment of inertia I about the pivot point can be expressed using the parallel axis theorem:
I=ICM+md2
where ICM=mL212 is the moment of inertia about the center of mass. Thus,
I=mL212+m(L2−x)2
4. Calculate the Torque:
The torque τ acting on the rod when displaced by a small angle θ is given by:
τ=−mgdθ
where g is the acceleration due to gravity.
5. Determine the Time Period T:
The time period of oscillation for a physical pendulum is given by:
T=2π√Imgd
6. Substituting I and d:
Substitute the expressions for I and d into the time period formula:
T=2π
⎷mL212+m(L2−x)2mg(L2−x)
7. Simplifying the Expression:
After simplification, we find:
T=2π
⎷L2/12+(L2−x)2g(L2−x)
8. Minimizing the Time Period:
To find the value of x that minimizes T, we can differentiate the expression inside the square root with respect to d (where d=L2−x) and set the derivative to zero:
dTdd=0
9. Solving for d:
After performing the differentiation and solving, we find:
d=L√12
10. Finding x:
Since d=L2−x, we can express x as:
x=L2−L√12=L2(1−1√3)
This simplifies to approximately:
x≈5L12
Final Answer:
Thus, the distance x from one end for minimum time period is approximately:
x≈5L12
The center of mass of a uniform rod of length L is located at a distance L2 from either end.
If the rod is suspended at a distance x from one end, then the distance d from the center of mass to the pivot point is:
d=∣∣∣L2−x∣∣∣
The moment of inertia I about the pivot point can be expressed using the parallel axis theorem:
I=ICM+md2
where ICM=mL212 is the moment of inertia about the center of mass. Thus,
I=mL212+m(L2−x)2
The torque τ acting on the rod when displaced by a small angle θ is given by:
τ=−mgdθ
where g is the acceleration due to gravity.
The time period of oscillation for a physical pendulum is given by:
T=2π√Imgd
Substitute the expressions for I and d into the time period formula:
T=2π
⎷mL212+m(L2−x)2mg(L2−x)
After simplification, we find:
T=2π
⎷L2/12+(L2−x)2g(L2−x)
To find the value of x that minimizes T, we can differentiate the expression inside the square root with respect to d (where d=L2−x) and set the derivative to zero:
dTdd=0
After performing the differentiation and solving, we find:
d=L√12
Since d=L2−x, we can express x as:
x=L2−L√12=L2(1−1√3)
This simplifies to approximately:
x≈5L12
Thus, the distance x from one end for minimum time period is approximately:
x≈5L12
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
A uniform rod of length l is suspended from a point P. and the rod is made to undergo small oxcillations. Match the following
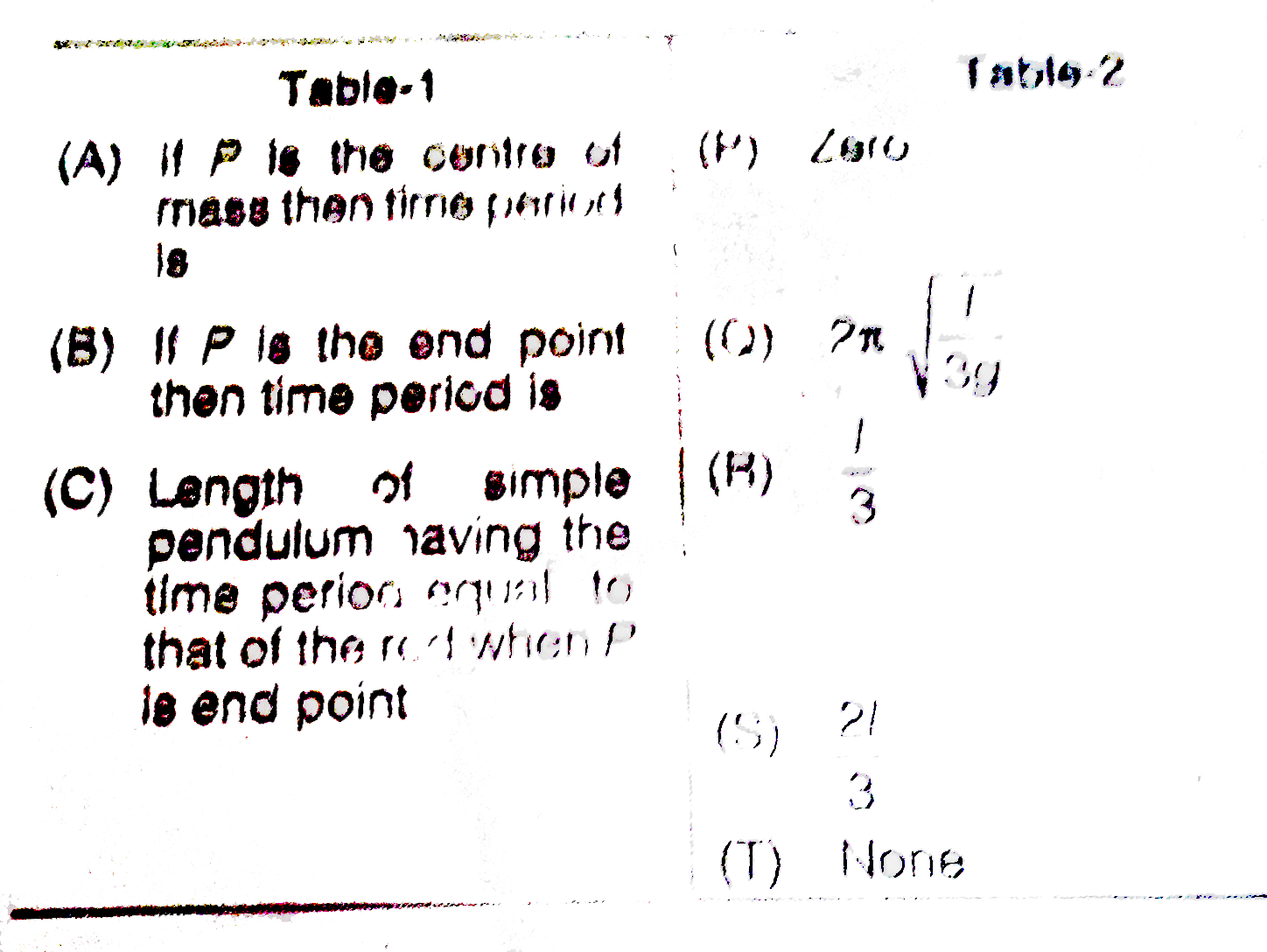
View SolutionA rod is of length 3 m and its mass acting per unit length is directly proportional to distance x from its one end. The centre of gravity of the rod from that end will be at
View SolutionA uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
View SolutionA uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA thin rod of length L is hanging from one end and free to oscillate like s compound pendulum about a horizontal axis, Its time period for small oscillations is
View Solution

