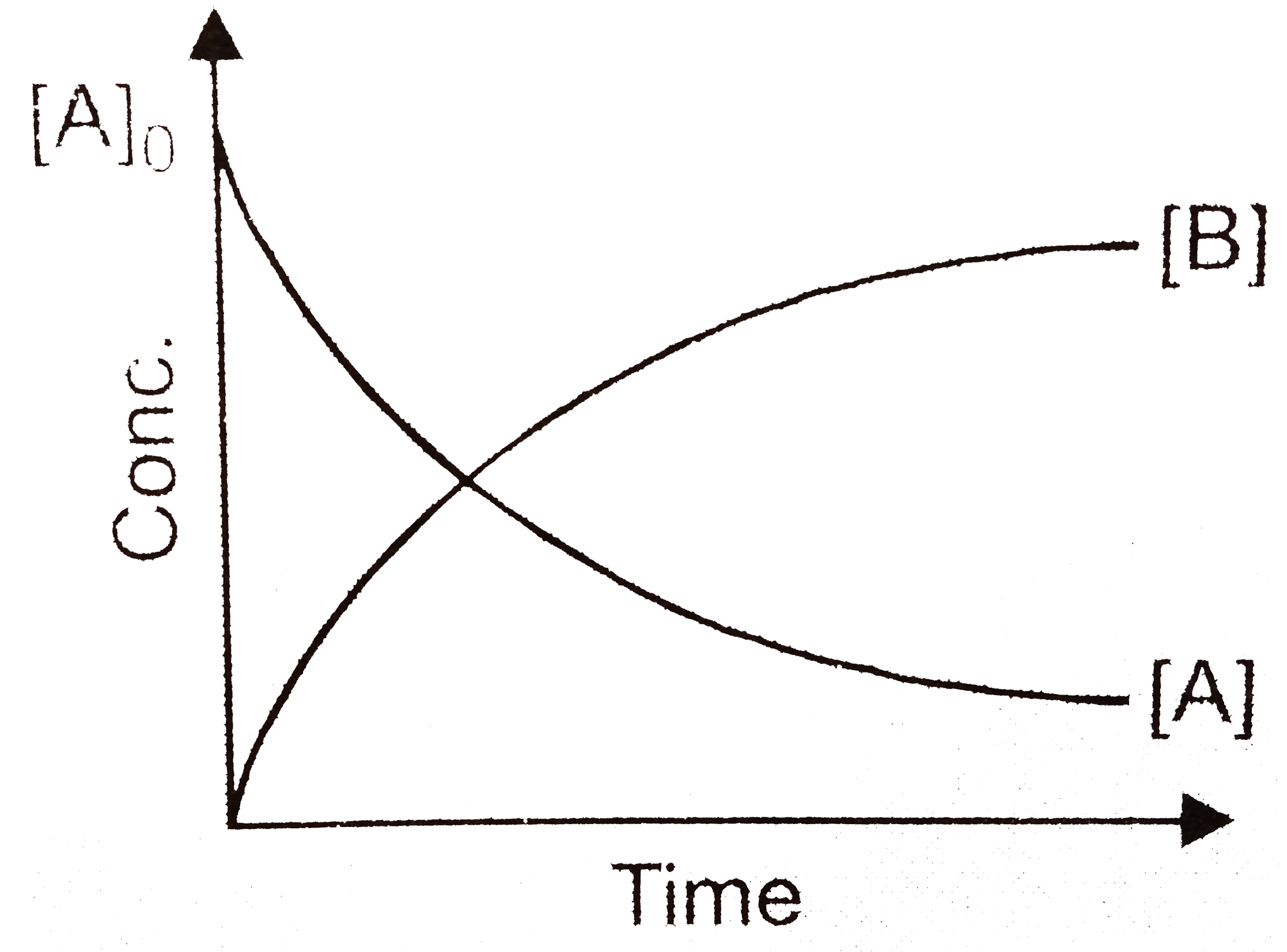
At the point of intersection of the two curves shown, the conc. of B is given by ……… for, A→nB:
nA02
A0n−1
nA0n+1
(n−1n+1)A0
The correct Answer is:C
From figure [A]left=[B]formed=n×[A]decayed
∴ [A]beλt=n×A0[1−e−λt]
∴ [B]formed=n×A0×[1−nn+1]
=nA0n+1
Topper's Solved these Questions
- CARBONYL COMPOUNDS (ALDEHYDES & KETONES ) & CARBOXYLIC ACID BOOK - RESONANCE ENGLISHCHAPTER - CARBONYL COMPOUNDS (ALDEHYDES & KETONES ) & CARBOXYLIC ACID EXERCISE - Part -IV
23 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - RESONANCE ENGLISHCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ORGANIC CHEMISTRY(Chemistry in every day life)
31 Videos
Similar Questions
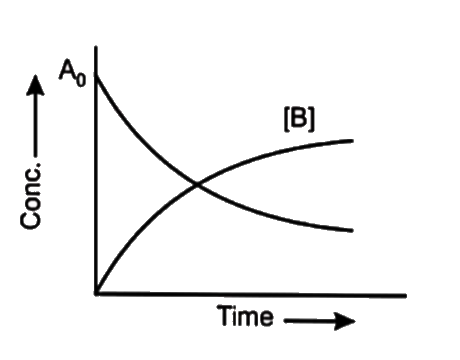
At the point of intersection of the two curves shown the concentration of B is given by _______for the first reaction A→nB.
View SolutionWrite the number of points in intersection of the curves 2y=−1andy=cosecx .
View SolutionAt the point of intersection of the curves y2=4ax and xy=c2, the tangents to the two curves make angles α and β respectively with x-axis. Then tanαcotβ=
View SolutionProve that the locus of the point of intersection of the normals at the ends of a system of parallel cords of a parabola is a straight line which is a normal to the curve.
View SolutionTwo poles of height a metres and b metres are p metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by aba+b metres.
View SolutionFind the point of intersection of the tangents drawn to the curve x2y=1−y at the points where it is intersected by the curve xy=1−y.
View SolutionWhich of the two curves shown below has lesser time constant.

View SolutionThe number of points of intersection of two curves y=2sinxandy=5x2+2x+3is 0 b. 1 c. 2 d. ∞
View SolutionThe abscissa of the point of intersection of the less that type of the more than type cumulative frequency curves of a grouped data gives its
View SolutionThe locus of the point of intersection of tangents drawn at the extremities of a normal chord to the parabola y2=4ax is the curve
View Solution
