For a complex reaction Ak−−→products
Ea1=180kJ/mole,Ea2=80kJ/mol,Ea3=50kJ/mol
Overall rate constant k is related to individual rate constant by the equation k=(k1k2k3)2/3. Activation energy (kJ/mol) for the overall reaction is :
100
43.44
150
140
The correct Answer is:4
To solve the problem of determining the activation energy for the overall reaction given the activation energies of individual steps and the relationship between the rate constants, we can follow these steps:
Step 1: Understand the given data
We are given:
- Activation energies for three steps:
- Ea1=180kJ/mol
- Ea2=80kJ/mol
- Ea3=50kJ/mol
- The overall rate constant k is related to the individual rate constants by the equation:
k=(k1k2k3)23
Step 2: Write the Arrhenius equation for each rate constant
The Arrhenius equation relates the rate constant k to the activation energy Ea:
k=Ae−EaRT
Where:
- A is the pre-exponential factor,
- R is the universal gas constant,
- T is the temperature in Kelvin.
For each step, we can write:
- k1=Ae−Ea1RT
- k2=Ae−Ea2RT
- k3=Ae−Ea3RT
Step 3: Substitute the rate constants into the overall rate constant equation
Substituting k1, k2, and k3 into the equation for k:
k=⎛⎜⎝Ae−Ea1RT⋅Ae−Ea2RTAe−Ea3RT⎞⎟⎠23
This simplifies to:
k=(A2e−Ea1+Ea2−Ea3RT)23
Step 4: Simplify the expression
Since A2 raised to 23 is A43:
k=A43e−23(Ea1+Ea2−Ea3RT)
Step 5: Compare with the Arrhenius equation for overall reaction
We can express the overall rate constant k as:
k=A′e−EaRT
Where Ea is the activation energy for the overall reaction.
Step 6: Equate the exponents
From the two expressions for k, we can equate the exponents:
−EaRT=−23(Ea1+Ea2−Ea3RT)
Step 7: Solve for Ea
Cancelling −1RT:
Ea=23(Ea1+Ea2−Ea3)
Step 8: Substitute the values
Now substituting the values of Ea1, Ea2, and Ea3:
Ea=23(180+80−50)
Calculating the expression inside the parentheses:
Ea=23(210)=140kJ/mol
Final Answer
The activation energy for the overall reaction is:
140kJ/mol
We are given:
- Activation energies for three steps:
- Ea1=180kJ/mol
- Ea2=80kJ/mol
- Ea3=50kJ/mol
- The overall rate constant k is related to the individual rate constants by the equation:
k=(k1k2k3)23
The Arrhenius equation relates the rate constant k to the activation energy Ea:
k=Ae−EaRT
Where:
- A is the pre-exponential factor,
- R is the universal gas constant,
- T is the temperature in Kelvin.
- k1=Ae−Ea1RT
- k2=Ae−Ea2RT
- k3=Ae−Ea3RT
Substituting k1, k2, and k3 into the equation for k:
k=⎛⎜⎝Ae−Ea1RT⋅Ae−Ea2RTAe−Ea3RT⎞⎟⎠23
This simplifies to:
k=(A2e−Ea1+Ea2−Ea3RT)23
Since A2 raised to 23 is A43:
k=A43e−23(Ea1+Ea2−Ea3RT)
We can express the overall rate constant k as:
k=A′e−EaRT
Where Ea is the activation energy for the overall reaction.
From the two expressions for k, we can equate the exponents:
−EaRT=−23(Ea1+Ea2−Ea3RT)
Cancelling −1RT:
Ea=23(Ea1+Ea2−Ea3)
Now substituting the values of Ea1, Ea2, and Ea3:
Ea=23(180+80−50)
Calculating the expression inside the parentheses:
Ea=23(210)=140kJ/mol
The activation energy for the overall reaction is:
140kJ/mol
Topper's Solved these Questions
- CARBONYL COMPOUNDS (ALDEHYDES & KETONES ) & CARBOXYLIC ACID BOOK - RESONANCE ENGLISHCHAPTER - CARBONYL COMPOUNDS (ALDEHYDES & KETONES ) & CARBOXYLIC ACID EXERCISE - Part -IV
23 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - RESONANCE ENGLISHCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ORGANIC CHEMISTRY(Chemistry in every day life)
31 Videos
Similar Questions
A reaction takes place in various steps. The rate constatn for first, second, third and fifth steps are k1,k2,k3 and k5 respectively The overall rate constant is given by
k=k2k3(k1k5)1/2
If activation energy are 40, 60, 50, and 10 kJ/mol respectively, the overall energy of activation (kJ/mol) is :
View SolutionRate constant for a chemical reaction taking place at 500K is expressed as K=A.e−1000 The activation energy of the reaction is :
View SolutionA reaction takes place in theee steps: the rate constant are k1,k2,andk3. The overall rate constant k=k1k3k2. If E1,E2, and E3 (energy of activation) are 60,30 and 10kJ, respectively, the overall energy of activation is
View SolutionFor following reactions
A400K−−→ Product
A200K−−−−−→catalyst Product
it was found that the Ea is decreased by 20 kJ/ mol in the presence of catalyst. If the rate remains unchanged, the activation energy for catalysed reaction is ( Assume per exponential factor is same ) :
View SolutionFor following reactions
A400K−−→ Product
A200K−−−−−→catalyst Product
it was found that the Ea is decreased by 20 kJ/ mol in the presence of catalyst. If the rate remains unchanged, the activation energy for catalysed reaction is ( Assume per exponential factor is same ) :
View SolutionA+B→C,ΔH=+60 kJ/mol
Eaf is 150 kJ. What is the activation energy for the backward reaction ?
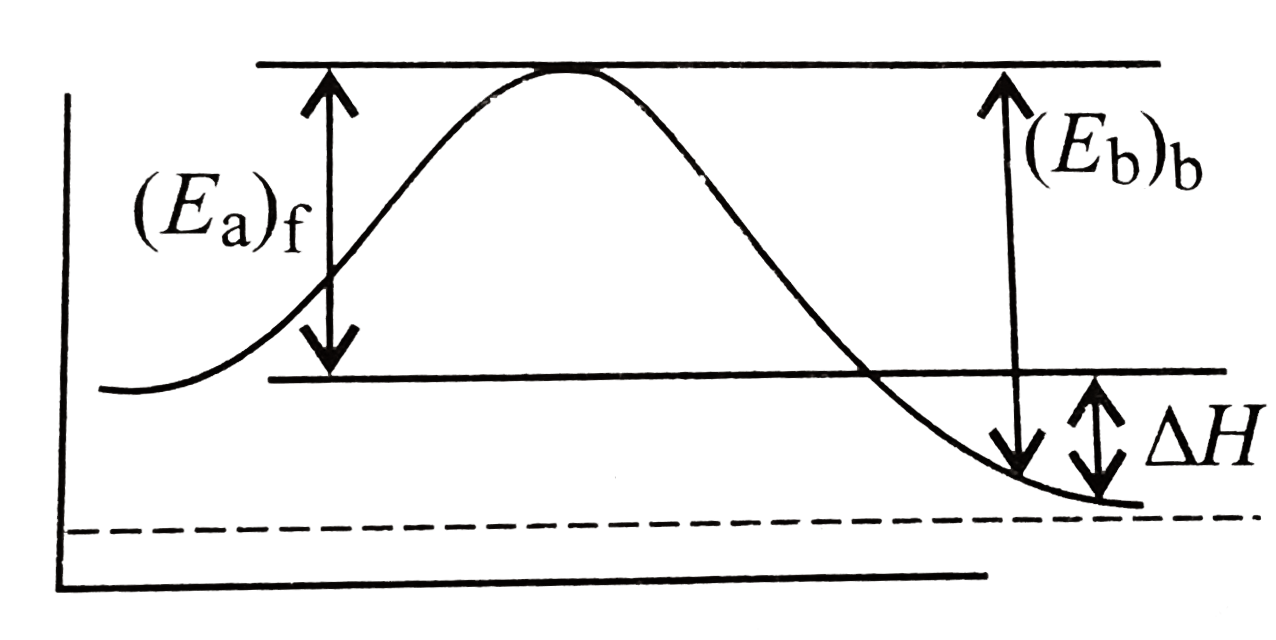
View SolutionIn an exothermic reaction X→Y, the activation energy is 100kJmol−1 of X. The enthalphy of the reaction is −140kJmol−1. The activation energy of the reverse reaction Y→X is
View SolutionA reaction takes place in theee steps: the rate constant are k1,k2,andk3. The overall rate constant k=k1k3/k2. If the energies of activation are 40,30,and20KJmol−1, the overall energy of activation is (assuming A to be constant for all)
View SolutionA reaction takes place in theee steps: the rate constant are k1,k2,andk3. The overall rate constant k=k1k3/k2. If the energies of activation are 40,30,and20KJmol−1, the overall energy of activation is (assuming A to be constant for all)
View SolutionFor the reaction at 300 K , A(g)→B(g)+E(g),ΔH∘=−30KJmol−1 , the decrease in standard entropy is 0.1KJK−1mol−1.The equilibrium constant K for the reaction is ________.
View Solution
