Calculate the final pressure of a sample of carbon dioxide that expands reversibly and adiabatically from 57.4kPa and 1.0 to a final volume of 2.0L . Take γ=1.4
1kPa
10kPa
20kPa
22kPa
The correct Answer is:2
To solve the problem of calculating the final pressure of a sample of carbon dioxide that expands reversibly and adiabatically, we can follow these steps:
Step 1: Understand the Adiabatic Process
In an adiabatic process, the relationship between pressure and volume is given by the equation:
P1Vγ1=P2Vγ2
where P1 and V1 are the initial pressure and volume, P2 and V2 are the final pressure and volume, and γ (gamma) is the heat capacity ratio.
Step 2: Identify Given Values
From the problem statement, we have:
- Initial Pressure, P1=57.4kPa
- Initial Volume, V1=1.0L
- Final Volume, V2=2.0L
- γ=1.4
Step 3: Substitute Values into the Equation
Using the adiabatic equation, we can substitute the known values:
57.4kPa×(1.0L)1.4=P2×(2.0L)1.4
Step 4: Rearrange to Solve for P2
Rearranging the equation to solve for P2:
P2=57.4kPa×(1.0L)1.4(2.0L)1.4
Step 5: Calculate the Final Pressure
Now, we can calculate P2:
1. Calculate (2.0)1.4:
(2.0)1.4≈2.639
2. Substitute this value back into the equation:
P2=57.4kPa2.639
3. Calculate P2:
P2≈21.7kPa
Step 6: Round the Final Answer
Rounding to two significant figures, we get:
P2≈22.0kPa
Final Answer
The final pressure of the carbon dioxide after the adiabatic expansion is approximately 22.0 kPa.
---
In an adiabatic process, the relationship between pressure and volume is given by the equation:
P1Vγ1=P2Vγ2
where P1 and V1 are the initial pressure and volume, P2 and V2 are the final pressure and volume, and γ (gamma) is the heat capacity ratio.
From the problem statement, we have:
- Initial Pressure, P1=57.4kPa
- Initial Volume, V1=1.0L
- Final Volume, V2=2.0L
- γ=1.4
Using the adiabatic equation, we can substitute the known values:
57.4kPa×(1.0L)1.4=P2×(2.0L)1.4
Rearranging the equation to solve for P2:
P2=57.4kPa×(1.0L)1.4(2.0L)1.4
Now, we can calculate P2:
1. Calculate (2.0)1.4:
(2.0)1.4≈2.639
2. Substitute this value back into the equation:
P2=57.4kPa2.639
3. Calculate P2:
P2≈21.7kPa
Rounding to two significant figures, we get:
P2≈22.0kPa
The final pressure of the carbon dioxide after the adiabatic expansion is approximately 22.0 kPa.
Topper's Solved these Questions
- THERMODYNAMIC & THERMOCHEMISTRYBook:RESONANCE ENGLISHChapter:THERMODYNAMIC & THERMOCHEMISTRYExercise:INORGANIC CHEMISTRY(P-Block Elements)
Explore 26 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBook:RESONANCE ENGLISHChapter:STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYExercise:Section -B
Explore 18 Videos
Similar Questions
Calculate the final temperature of a monoatomic ideal gas that is compressed reversible and adiabatically from 16L to 2L at 300K:
View SolutionCalculate the entropy change when 1mole of an ideal gas expands reversibly form an initial volume of 2L to a final voluume of 20L at 25∘C.
View SolutionCalculate entropy change when 10mol of an ideal gas expands reversible and isothermally from an initial volume of 10L to 100L at 300K.
View SolutionCalculate the work done (in joules) when 0.2 mole of an ideal gas at 300K expands isothermally and reversible from an initial volume of 2.5 litres to the final volume of 25 litres.
View SolutionWhat will be the final volume of a mole of an idela gas at 20∘C when it expands adiabatically from a volume of 5L at 30∘C?CV of the gas =5cal/degree.
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
Which relation is correct (γ=CPCV)?
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) is
View SolutionA monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take γ=53)
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, then
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which graphic representation is correct
a.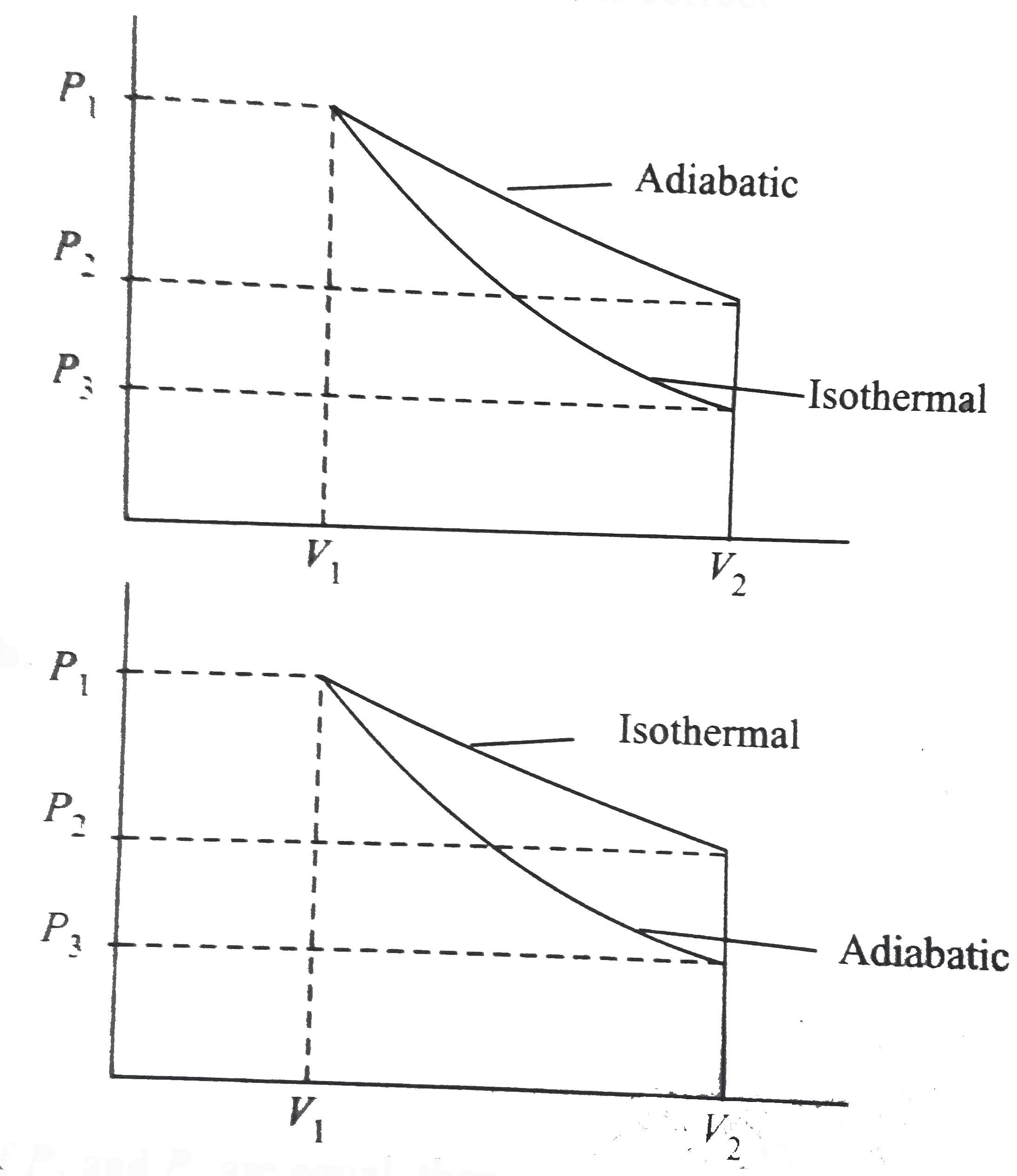
View Solution

