A 100ml solution having activity 50 dps is kept in a beaker It is now constantly diluted by adding water at a constant rate of and of solution is constantly being taken out. Find the activity of 10 ml solution which is taken out, assuming half life to be effectively very large :
The correct Answer is: where
To solve the problem, we need to find the activity of the 10 ml solution that is taken out from a beaker containing a radioactive solution. The initial conditions are as follows:
- Initial volume of the solution = 100 ml
- Initial activity of the solution (A₀) = 50 dps
- Rate of water being added = 10 ml/sec
- Rate of solution being taken out = 2 ml/sec
- We need to find the activity of the solution taken out after a certain time.
1. Determine the total volume of the solution at any time t:
V(t)=100 ml+(10 ml/sec×t)−(2 ml/sec×t)=100+8t ml
2. Determine the activity of the solution at any time t:
The activity of the solution is proportional to the number of radioactive nuclei present. Since we are assuming the half-life is very large, the activity will not change significantly over short periods. Therefore, we can use the initial activity A₀ and the dilution factor.
3. Calculate the time to take out 10 ml of the solution:
Since the solution is being taken out at a rate of 2 ml/sec, the time t to take out 10 ml is:
t=10 ml2 ml/sec=5 seconds
4. Calculate the activity at t=5 seconds:
The activity at any time t can be derived from the formula:
A(t)=A₀(V₀V(t))
where V₀ is the initial volume (100 ml) and V(t) is the volume at time t:
V(5)=100+8×5=140 ml
Thus, the activity at t=5 seconds is:
A(5)=50(100140)=50×57=2507 dps
5. Calculate the activity of the 10 ml solution taken out:
The activity of the 10 ml solution taken out is given by:
Aout=A(5)×10 mlV(5)=2507×10140
Simplifying this gives:
Aout=2500980=12549 dps
Final Answer:
The activity of the 10 ml solution taken out is approximately 2.55 dps.
- Initial activity of the solution (A₀) = 50 dps
- Rate of water being added = 10 ml/sec
- Rate of solution being taken out = 2 ml/sec
- We need to find the activity of the solution taken out after a certain time.
V(t)=100 ml+(10 ml/sec×t)−(2 ml/sec×t)=100+8t ml
The activity of the solution is proportional to the number of radioactive nuclei present. Since we are assuming the half-life is very large, the activity will not change significantly over short periods. Therefore, we can use the initial activity A₀ and the dilution factor.
Since the solution is being taken out at a rate of 2 ml/sec, the time t to take out 10 ml is:
t=10 ml2 ml/sec=5 seconds
The activity at any time t can be derived from the formula:
A(t)=A₀(V₀V(t))
where V₀ is the initial volume (100 ml) and V(t) is the volume at time t:
V(5)=100+8×5=140 ml
Thus, the activity at t=5 seconds is:
A(5)=50(100140)=50×57=2507 dps
The activity of the 10 ml solution taken out is given by:
Aout=A(5)×10 mlV(5)=2507×10140
Simplifying this gives:
Aout=2500980=12549 dps
The activity of the 10 ml solution taken out is approximately 2.55 dps.
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise -3 Part-III CBSE PROBLEMS (LAST 10 YEARS)
34 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
- REVISION DPPBOOK - RESONANCE ENGLISHCHAPTER - REVISION DPPEXERCISE - All Questions
463 Videos
Similar Questions
1.11gCaCl2 is added to water forming 500ml of solution 20ml of this solution is taken and diluted 10 folds Find moles of Cl ions in 2ml of diluted solution .
View SolutionWhat will be the Molarity of solution when water is added to 10gCaCO3 to make 100mL of solution ? .
View SolutionThe coagulation of 100mL of a colloidal solution of gold is completely prevented by the addition of 0.030g of it before adding 1mL of 10%NaCl solution. Find out the gold number of starch?
View SolutionThe coagulation of 100mL of a colloidal solution of gold is completely prevented by the addition of 0.030g of it before adding 1mL of 10%NaCl solution. Find out the gold number of starch?
View SolutionKa for HCN is 5×10−10 at 25∘C. For maintaining a constant pH of 9.0, the volume of 5MKCN solution required to be added to 10mL of 2MHCN solution is
View SolutionWhat volume of 2 N HCI be taken to form 500 mL N10 solution of HCl?
View SolutionTo a 50 ml of 0.1 M HCl solution , 10 ml of 0.1 M NaOH is added and the resulting solution is diluted to 100 ml. What is change in pH of the HCl solution ?
View SolutionIn three beakers labelled as (A),(B) and (C ) , 100 mL of water, 100 mL of 1 M solution of glucose in water and 100 mL of 0.5 M solution of glucose in water are taken respectively and kept at same temperature .
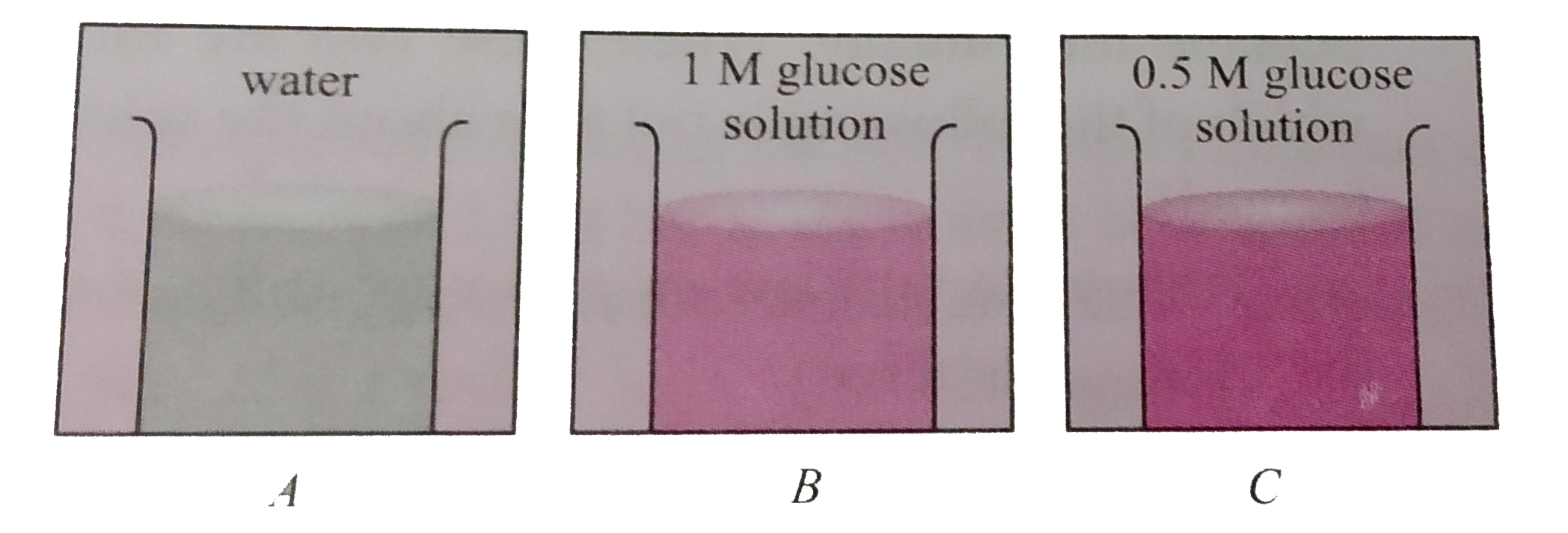
Which of the following statements is correct ?
View Solution3 gram of acetic acid is mixed in 250 mL of 0.1 M HCl. This mixture is now diluted to 500 mL. 20 mL of this solution is now taken is another container 12 mL of 5M NaOH is added to this. Find the pH of this solution. (pKa=4.74)
View SolutionThe activity per ml of a solution of radioactive substances is x.How much water be added to 200 ml of this so that the acitivity falls to x//20 per ml after 4 half-lives ?
View Solution
