Force acting upon charged particle kept between the plates of a charged condenser is F. If one of the plates of the condenser is removed, force acting on the same particle will become.
0
F2
F
2F
The correct Answer is:B
To solve the problem, we need to understand the concept of electric fields and forces acting on charged particles in a capacitor.
1. Understanding the Initial Setup:
- We have a parallel plate capacitor with two plates: one positively charged and one negatively charged.
- The electric field (E) between the plates is uniform and directed from the positive plate to the negative plate.
2. Calculating the Electric Field:
- The electric field (E) between two plates of a capacitor is given by:
E=Vd
where V is the voltage across the plates and d is the separation between them.
- In the case of a parallel plate capacitor, the net electric field between the plates is:
Enet=E+E=2E
3. Force on the Charged Particle:
- If a charge q is placed between the plates, the force F acting on the charge due to the electric field is given by:
F=q⋅Enet=q⋅2E
- Thus, the initial force F is:
F=2qE
4. Removing One Plate:
- When one of the plates is removed, only the electric field from the remaining plate is present.
- The electric field due to a single charged plate is given by:
E=σ2ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
- Therefore, the electric field E′ acting on the charge q now becomes:
E′=E
5. Calculating the New Force:
- The new force F′ acting on the charge q when one plate is removed is:
F′=q⋅E′=q⋅E
6. Finding the Relationship Between Forces:
- Now, we can relate the new force F′ to the original force F:
F′=F2
- This shows that the new force is half of the original force.
Conclusion:
The force acting on the charged particle after one plate of the capacitor is removed becomes:
F′=F2
- We have a parallel plate capacitor with two plates: one positively charged and one negatively charged.
- The electric field (E) between the plates is uniform and directed from the positive plate to the negative plate.
- The electric field (E) between two plates of a capacitor is given by:
E=Vd
where V is the voltage across the plates and d is the separation between them.
- In the case of a parallel plate capacitor, the net electric field between the plates is:
Enet=E+E=2E
- If a charge q is placed between the plates, the force F acting on the charge due to the electric field is given by:
F=q⋅Enet=q⋅2E
- Thus, the initial force F is:
F=2qE
- When one of the plates is removed, only the electric field from the remaining plate is present.
- The electric field due to a single charged plate is given by:
E=σ2ϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
- Therefore, the electric field E′ acting on the charge q now becomes:
E′=E
- The new force F′ acting on the charge q when one plate is removed is:
F′=q⋅E′=q⋅E
- Now, we can relate the new force F′ to the original force F:
F′=F2
- This shows that the new force is half of the original force.
The force acting on the charged particle after one plate of the capacitor is removed becomes:
F′=F2
Topper's Solved these Questions
Similar Questions
On placing dielectric slab between the plates of an isolated charged condenser its
View SolutionOne of the forces acting on the particle is conservative, then
View SolutionFour forces acting on a particle keep it in equilibrium, then :-
View SolutionThe magnitude of charge in steady state on either of the plates of condenser C in the adjoining circuit is

View SolutionCalculate the net force acting on the charge present at the origin.
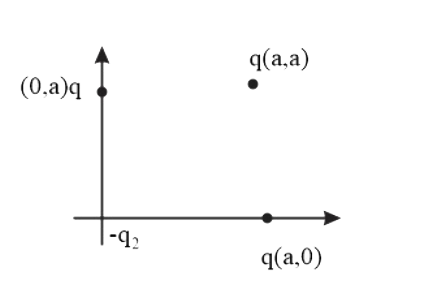
View SolutionIf a charged particle kept at rest experiences an electromagnetic force,
View SolutionThe separation between the plates of a charged parallel-plate capacitor is increased. The force between the plates
View SolutionA charged particle having charge q is moving in a uniform magnetic field B parallel to the lines of field force, the magnetic force acting on a charge will be qvB
View SolutionIf a constant force acts on a particle, its acceleration will
View SolutionA given charge is situated at a certain distance from an electric dipole in the end-on position experiences a force F If the distance of the charge is doubled, the force acting on the charge will be
View Solution
