When a wire of uniform cross-section a , length l and resistance R is bent into a complete circle, resistance between two of diametrically opposite points will be
R4
R8
4R
R2
The correct Answer is:A
When wire is bent to form a complete circle then
2πr=R⇒r=R2π
Resistance of each semicircle =πr=πR2π=R2
Thus, net resistance in parallel combination of two semicircular resistance
R'=R2×R2R2+R2=R24R=R4

Topper's Solved these Questions
Similar Questions
When a wire of uniform cross-section a, length I and resistance R is bent into a complete circle, resistance between two of diametrically opposite points will be
View SolutionA wire of resistance 10(Ω)is bent to form a complete circle.Find its resistance between two diametrically opposite points.
View Solution
Knowledge Check
A wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is
 A3ΩB6πΩC6ΩD0.6πΩ
A3ΩB6πΩC6ΩD0.6πΩ
A wire of resistance 20Ω is bent to form a complete circle. The resistance between two diametrically opposite points A and B as shown in the figure, is
View SolutionA metallic wire having a resistance of 20Ω is bent in order to form a complete circle. Calculate the resistance between any two diametrically opposite points on the circle.
View SolutionA uniform wire os resistance 12Ω is bent to form a circle. Effective resistance across two diametrically opposite points is
View SolutionA wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is

View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
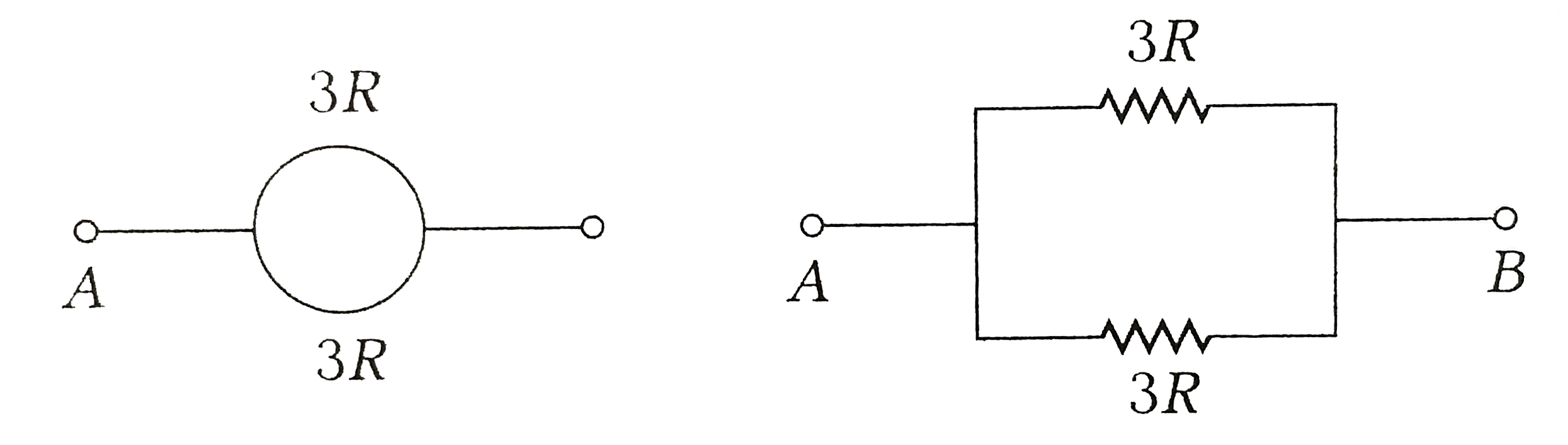
View SolutionA battery is connected across a resistance wire of uniform cross-section . If another resistance wire is connected in parallel, then the intensity of electric field in the first wire will
View SolutionA wire of resistance 4Ω is bent to form a circle. The resistance point A and B will be
_PHY_E05_303_Q01.png)
View Solution

