A source of frequency 'f' is stationary and an obsercer starts moving towards it at t=0 with constant small acceleration. Then the variation of observed frequency 'f' registered by the observer with time is best represented as




The correct Answer is:A
To solve the problem, we need to analyze how the observed frequency changes as the observer moves towards a stationary sound source with constant small acceleration. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Doppler Effect
The Doppler effect describes how the frequency of a wave changes for an observer moving relative to the source of the wave. In this case, the source is stationary, and the observer is moving towards it.
Step 2: Define the Variables
Let:
- f = frequency of the stationary source
- v = speed of sound in the medium
- a = constant acceleration of the observer
- t = time
- v0 = velocity of the observer at time t
Step 3: Determine the Velocity of the Observer
Since the observer starts from rest and accelerates with a constant acceleration a, the velocity of the observer at time t can be expressed as:
v0=a⋅t
Step 4: Apply the Doppler Effect Formula
The observed frequency f1 when the observer is moving towards the source can be given by the formula:
f1=f⋅v+v0v
Substituting v0 from Step 3:
f1=f⋅v+a⋅tv
Step 5: Simplify the Expression
This can be simplified to:
f1=f+a⋅fv⋅t
This shows that the observed frequency f1 is a linear function of time t.
Step 6: Identify the Relationship
The equation f1=f+a⋅fv⋅t indicates that:
- The frequency increases linearly with time.
- The slope of the line is a⋅fv, which is positive since a, f, and v are all positive.
Step 7: Graphical Representation
The relationship between observed frequency f1 and time t can be represented graphically as a straight line with:
- A positive slope (indicating increasing frequency)
- A positive intercept (the frequency at t=0 is f)
Conclusion
Thus, the variation of the observed frequency f1 registered by the observer with time is best represented as a straight line with a positive slope and a positive intercept.
The Doppler effect describes how the frequency of a wave changes for an observer moving relative to the source of the wave. In this case, the source is stationary, and the observer is moving towards it.
Let:
- f = frequency of the stationary source
- v = speed of sound in the medium
- a = constant acceleration of the observer
- t = time
- v0 = velocity of the observer at time t
Since the observer starts from rest and accelerates with a constant acceleration a, the velocity of the observer at time t can be expressed as:
v0=a⋅t
The observed frequency f1 when the observer is moving towards the source can be given by the formula:
f1=f⋅v+v0v
Substituting v0 from Step 3:
f1=f⋅v+a⋅tv
This can be simplified to:
f1=f+a⋅fv⋅t
This shows that the observed frequency f1 is a linear function of time t.
The equation f1=f+a⋅fv⋅t indicates that:
- The frequency increases linearly with time.
- The slope of the line is a⋅fv, which is positive since a, f, and v are all positive.
The relationship between observed frequency f1 and time t can be represented graphically as a straight line with:
- A positive slope (indicating increasing frequency)
- A positive intercept (the frequency at t=0 is f)
Thus, the variation of the observed frequency f1 registered by the observer with time is best represented as a straight line with a positive slope and a positive intercept.
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Solved Examples
24 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Board Level Exercise
33 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
A source emitting a sound of frequency f is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
View SolutionTwo identical source moving parallel to each other at seperation 'd' are producing sounds of frequency 'f' and are moving with constant velocity v0. A stationary .observer 'O' is on the line of motion of one of the sources. Then the variation of beat frequency heard by O with time is best represented by: (as they come from large distance and go to a large distance)
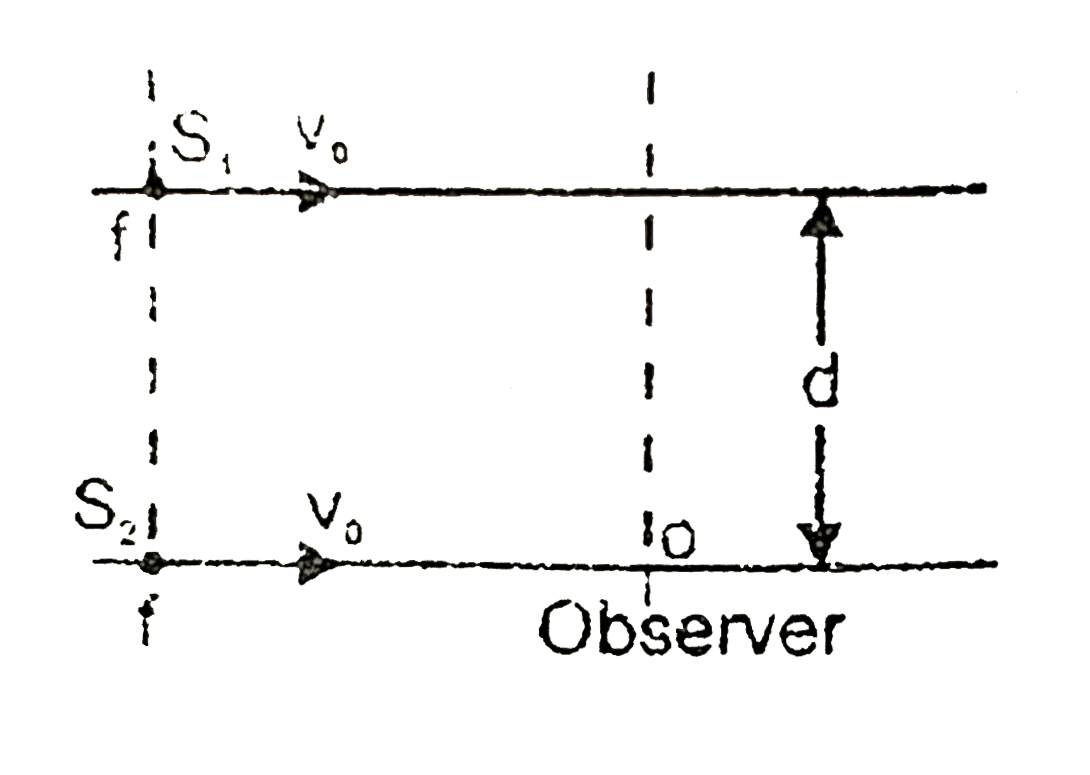
View Solution
Knowledge Check
A sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
A109B(109)2C(1110)2D1110To a stationary man the frequency of a sound source moving towards the man appears to be
Alower than the original frequencyBsame as the original frequencyChigher than the original frequencyDlower as well as higher than the original frequency depending upon the speed of the source.
A sound source S is moving along a straight track with speed v, and is emitting sound of frequency v0 (see figure). An observer is standing at a finite distance at the point O, from the track . The time variation of frequency heard by the observer is best respresent by :
(t0 represents the instant when the distance between the source and observer is minimum )
View SolutionAn observer moves with a constant acceleration towards a fixed source and start decelerating as soon as it passes the sound source. The variation of frequency f by observer with time t is best shown by
View SolutionA source of frequency f is moving towards the observer along the line SO with a constant velocity υs as shown in figure. Plot f' versus t graph . Where f' is the changed frequency observed by the observer.

View SolutionWhen both the listener and source are moving towards each other, then which of the following is true regarding frequency and wavelength of wave observed by the observer?
View SolutionA train is moving towards a stationary observer. Which of the following curve best represents the frequency recived by observer f as a function of time?
View SolutionA train whistling at constant frequency is moving towards a station at a constant speed V. The train goes past a stationary observer on the station. The frequency n′ of the sound as heard by the observer is plotted as a function of time t, figure. Identify the expected curve.
View Solution
