A vibrating string of certain length l under a tension T resonates with a mode corresponding to the first overtone (third harmonic) of an air column of length 75 cm inside a tube closed at one end. The string also generates 4 beats per second when excited along with a tuning fork of frequency n. Now when the tension of the string is slightly increased, the number of beats reduces to 2 per second. Assuming the velocity of sound in air to be 340 m/s, the frequency n of the tuning fork in Hz is
344
336
117.3
109.3
The correct Answer is:A
As string and tube are in resonance f1=f2
|f1−n|=4Hz.
When T increase, f1 also increases. It is given that beat frequency decreases to 2Hz.
⇒n−f1=4
n=4+f1
as f1=f2
n=4+f2
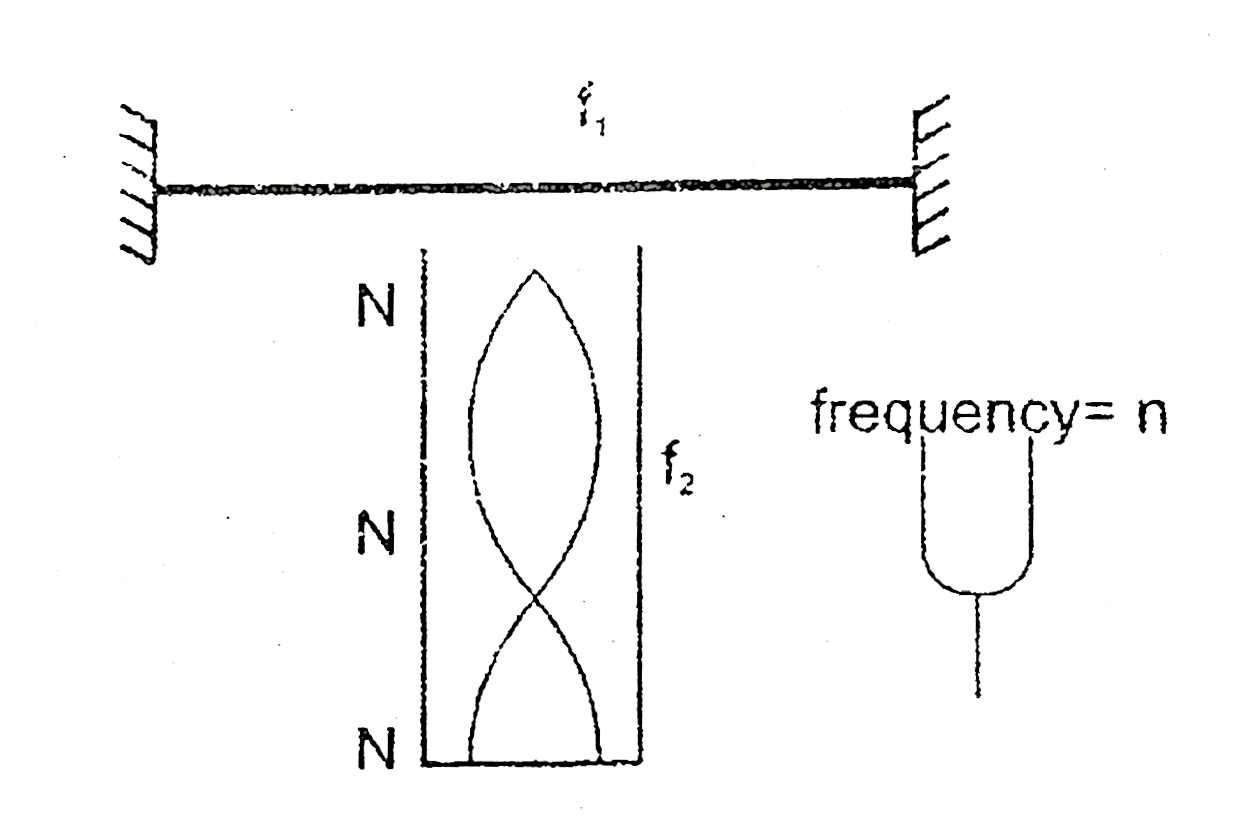
n=(4+f2)
f2=3V4l=3×3404×(3/4)=340
n=344
Topper's Solved these Questions
Similar Questions
A vibrating string of certain length l under a tension T resonates with a mode corresponding to the first overtone (third harmonic) of an air column of length 75cm inside a tube closed at one end. The string also generates 4 beats per second when excited along with a tuning fork of frequency n. Now when the tension of the string is slightly increased the number of beats reduces 2 per second. Assuming the velocity of sound in air to be 340m/s, the frequency n of the tuning fork in Hz is
View SolutionA vibrating string of certain length l under a tension T resonates with a mode corresponding to the first overtone (third harmonic ) of an air column of length 75cm inside a tube closed at one end. The string also generates 4beats/s with a tuning fork of frequency n . Now when the tension of the string is slightly increased the number of beats reduces to 2 per second. Assuming the velocity of sound in air to 340m/s , the frequency n the tuning fork in HZ is
(a) 344
(b) 336
(c ) 117.3
(d) 109.3
View Solution
Knowledge Check
Two sitar strings A and B are slightly out of tune and produce beats of frequency 5 Hz. When the tension in the string B is slightly increased, the beat frequency is found to reduce to 3 Hz. If the frequency of string A is 427 Hz, the original frequency of string B is
A422 HzB424 HzC430 HzD432 Hz
A tuning fork of frequency 340 Hz produces 5 beats per second with a sonometer wire. If the tension is slightly increased the number of beats becomes 4. The frequency of sonometer wire is
View SolutionA vibrating string produces 2 beats per secod when sounded with a turning fork of frequency 256Hz. Slightly increasing the tension in the string produces 3 beats per second. The initial frequency of the string may have been
View SolutionA string under a tension of 129.6 N produces 10 beats per sec when it is vibrated along with a tuning fork. When the tension in the string is increased to 160 N, it sounds in unison with the same tuning fork, Calculate the fundamental frequency of the tuning fork.
View SolutionThe string of violin emits a note of 440 Hz at its correct tension. The string is bit taut and produces 4 beats per second with a tuning fork of frequency 440 Hz. Find the frequency of the note emitted by this taut string.
View SolutionA tuning fork of frequency 510 Hz is vibrated with a sonometer wire and 4 beats per second are heard. The beat frequency increases if the tension in the string is slightly increased. The original frequency of the string is
View SolutionA column of air at 51∘C and a tuning fork produce 4 beats per second when sounded together. As the temperature of the air column is decreased, the number of beats per second tends to decrease and when the temperature is 16∘C the two produce 1 beat per second. Find the frequency of the tuning fork.
View SolutionA column of air at 51∘C and a tuning fork produce 4 beats per second when sounded together. As the temperature of the air column is decreased, the number of beats per second tends to decrease and when the temperature is 16∘C the two produce 1 beat per second. Find the frequency of the tuning fork.
View Solution

