A rectangular block has a square base measuring a×a and its height is h. It moves on a horizontal surface in a direction perpendicular to one of the edges. The coefficient of friction is μ. It will topple if
μ>ha
μ>ah
μ>2ah
μ>a2h
The correct Answer is:B
To determine the condition under which a rectangular block with a square base will topple when moving on a horizontal surface, we can follow these steps:
1. Identify the Forces Acting on the Block:
- The gravitational force (weight) acting downward, W=mg.
- The normal force N acting upward, which balances the weight, so N=mg.
- The frictional force F acting in the direction opposite to the motion, given by F=μN=μmg.
2. Understand the Toppling Condition:
- The block will start to topple when the torque due to the frictional force about the pivot point (the edge of the base) exceeds the torque due to the weight of the block acting through its center of mass.
3. Calculate the Torque Due to Friction:
- The torque τf due to the frictional force about the pivot point is given by:
τf=F⋅h2=μmg⋅h2
4. Calculate the Torque Due to Weight:
- The torque τw due to the weight of the block about the pivot point is given by:
τw=mg⋅a2
5. Set Up the Condition for Toppling:
- The block will start to topple when the torque due to friction equals the torque due to the weight:
τf>τw
- Thus, we have:
μmg⋅h2>mg⋅a2
6. Simplify the Equation:
- Cancel mg from both sides:
μ⋅h2>a2
- This simplifies to:
μh>a
7. Final Condition for Toppling:
- Rearranging gives:
μ>ah
Conclusion:
The rectangular block will start to topple if the coefficient of friction μ is greater than the ratio of the base side length a to the height h:
μ>ah
- The gravitational force (weight) acting downward, W=mg.
- The normal force N acting upward, which balances the weight, so N=mg.
- The frictional force F acting in the direction opposite to the motion, given by F=μN=μmg.
- The block will start to topple when the torque due to the frictional force about the pivot point (the edge of the base) exceeds the torque due to the weight of the block acting through its center of mass.
- The torque τf due to the frictional force about the pivot point is given by:
τf=F⋅h2=μmg⋅h2
- The torque τw due to the weight of the block about the pivot point is given by:
τw=mg⋅a2
- The block will start to topple when the torque due to friction equals the torque due to the weight:
τf>τw
- Thus, we have:
μmg⋅h2>mg⋅a2
- Cancel mg from both sides:
μ⋅h2>a2
- This simplifies to:
μh>a
- Rearranging gives:
μ>ah
The rectangular block will start to topple if the coefficient of friction μ is greater than the ratio of the base side length a to the height h:
μ>ah
Topper's Solved these Questions
Similar Questions
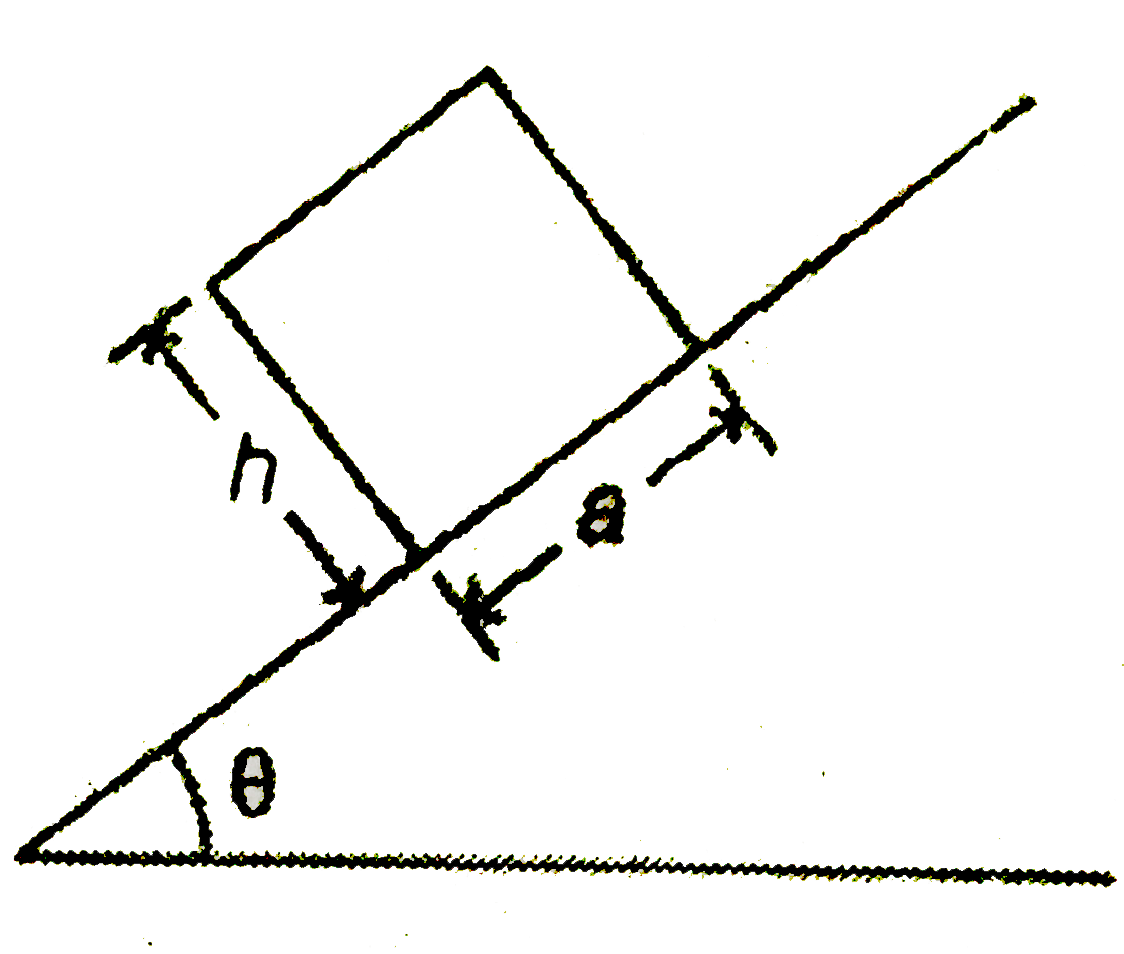
A block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
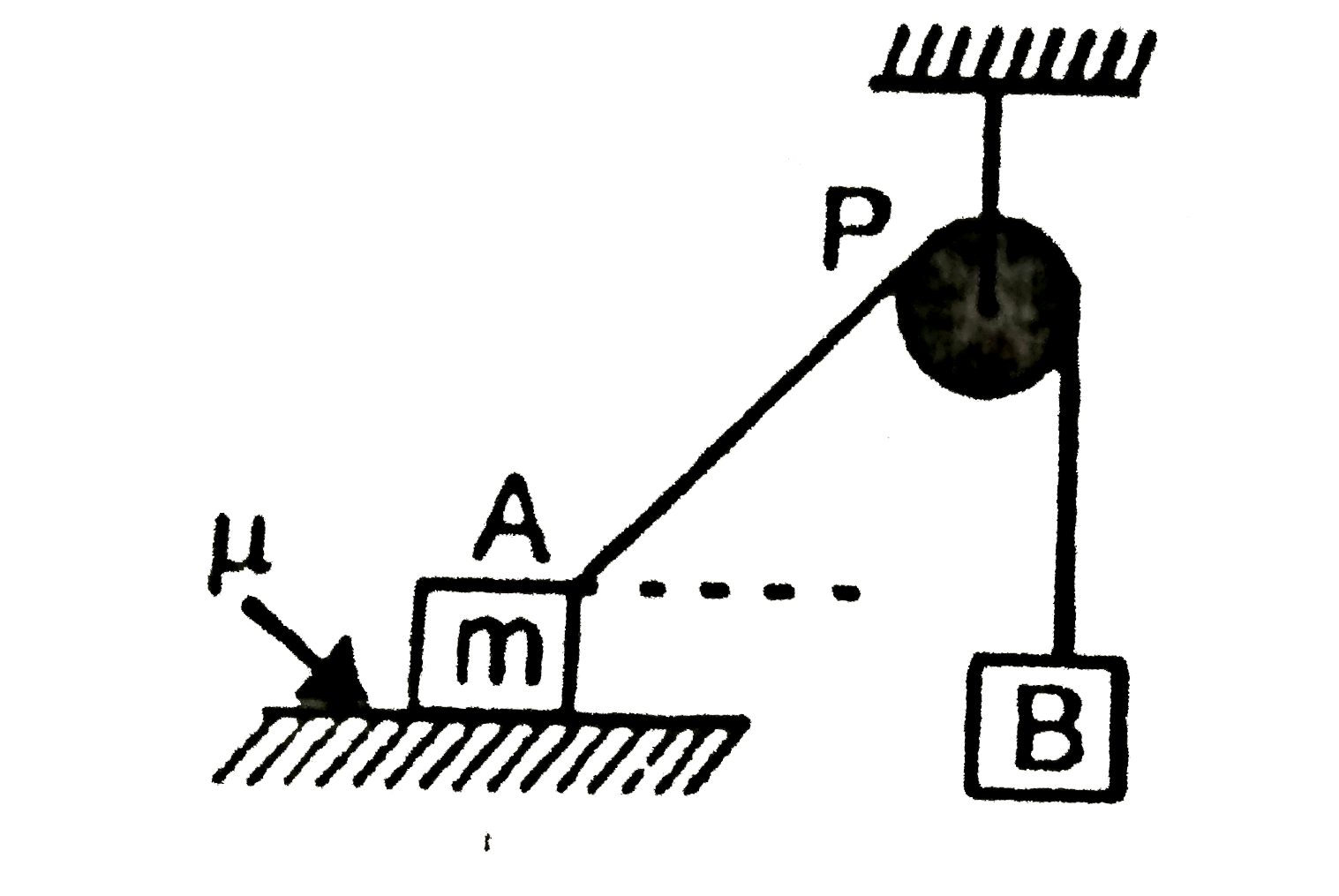
View SolutionIn figure shown minimum mass of block B( at a particular angle between horizontal and string AP) to just slide the block A on rough horizontal surface is m2 as shown in figure. If μ is the coefficient of friction between block A and ground then pμ2 will be :
View SolutionA sufficiently long plane of mass 4kg is placed on a smooth horizontal surfaces A small block of mass 2kg is placed over the plank and is being acted upon by a time varying horizontal force F=(0.5t) where F is in newton and t is in second as shown in figure. The coefficient of friction slipping the plank and the block is given is μs=μk=μ, at time t=12s the relative slipping between the plank and the block is just likely to occur

The coefficient of friction μ is equal to
View SolutionFind value of pulling force F for which block just moves. Given coefficient of friction for surface is μ.
View SolutionA varying horizontal force F= at act on a block of mass m kept on a smooth horizontal surface An identical block is kept on the first block. The coefficient of friction between the blocks is μ . The time after which the relative sliding between the blocks prevails is
View Solution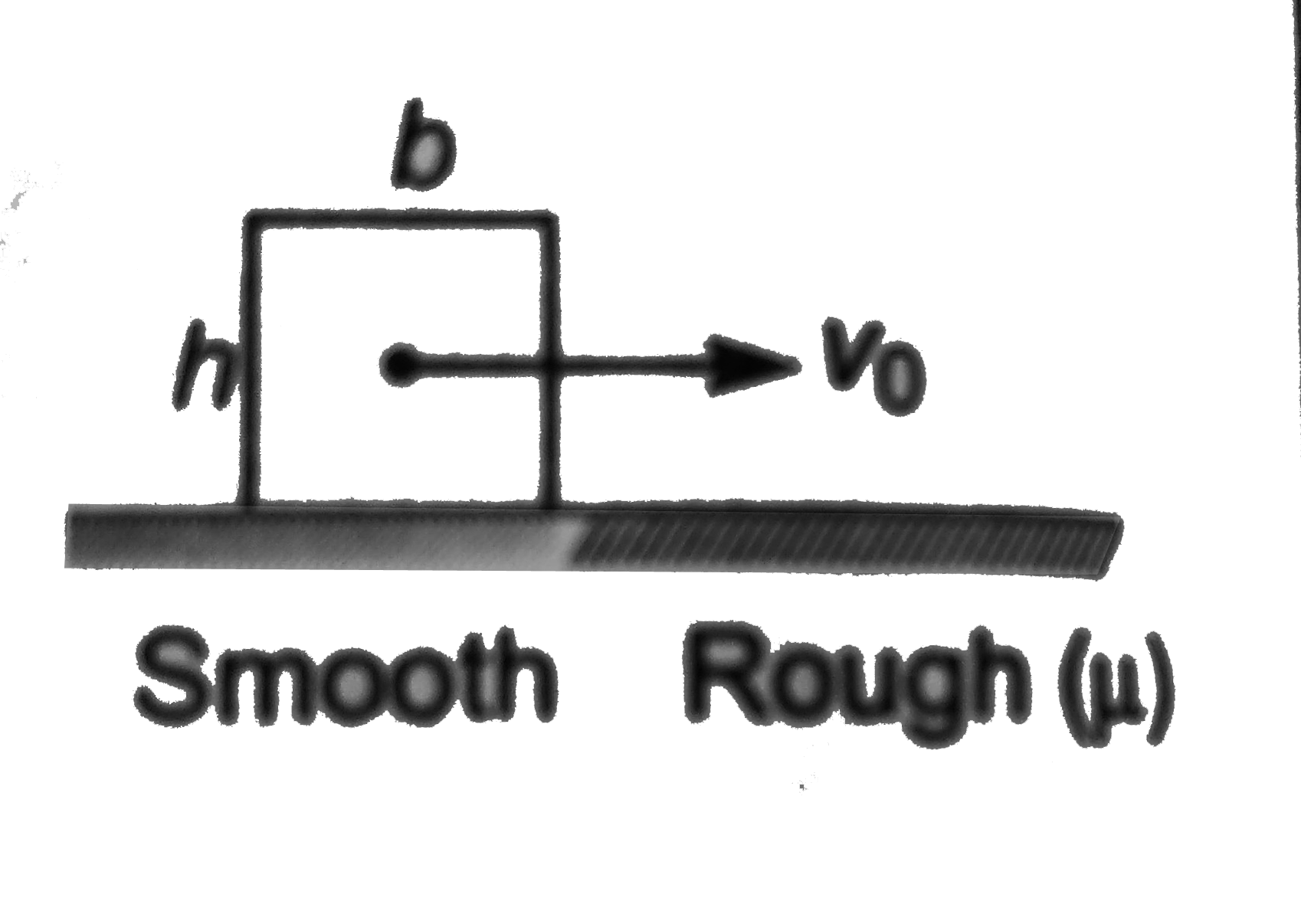
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.
View SolutionA force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
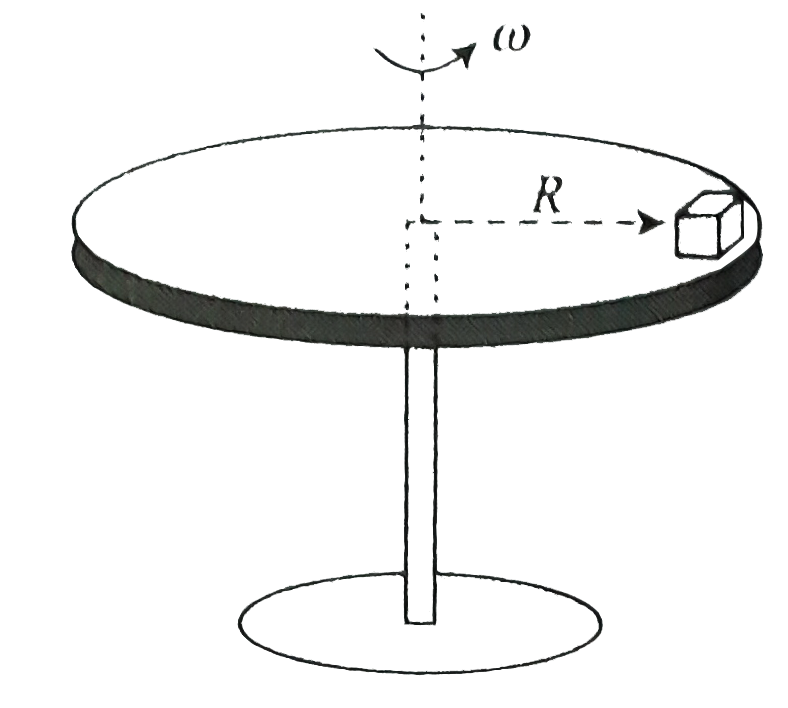
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionTwo blocks, each of mass m are attached with a massless and inextensible string. One of the blocks is placed on the rough horizontal surface of a table for which coefficient of friction μ. Find out the force exerted by the table on the block if μ>1.

View Solution

