Figure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
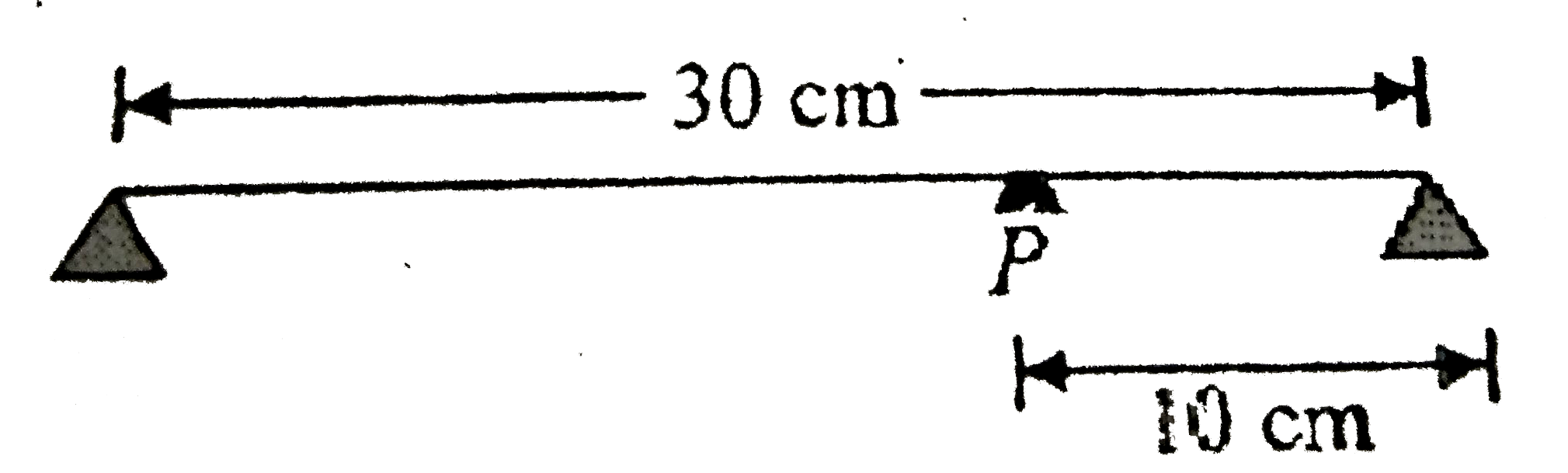
Now if the tension in the string is made 160N, at which of the following frequencies of turning fork , rider will not vibrate at all
1003Hz
100Hz
200Hz
None of these
The correct Answer is:C
Wave velocity in string is
V=√Tμ=√400.1=20m/s
Fundamental frequency of string oscillations is
n0=v2e=200.6=1003Hz
Thus string will be in resonance with a turning fork of frequency
nf=1003Hz,2003Hz,100Hz,4003Hz....
Here rider will not oscillate at all only if it is at a node of stationary wave in all other cases of resonance and non-resonance it will vibrate at the frequency of tuning fork. At a distance l3 from one end node will appear at 3rd,6th,9th similar higher Harmonics i.e. at frequencies 100 Hz,200 Hz
If string is divided in odd no of segments these segments can never resonance simultaneously hence at the location of rider antinode is never obtained at any frequency.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.69
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.70
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.67
10 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Figure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
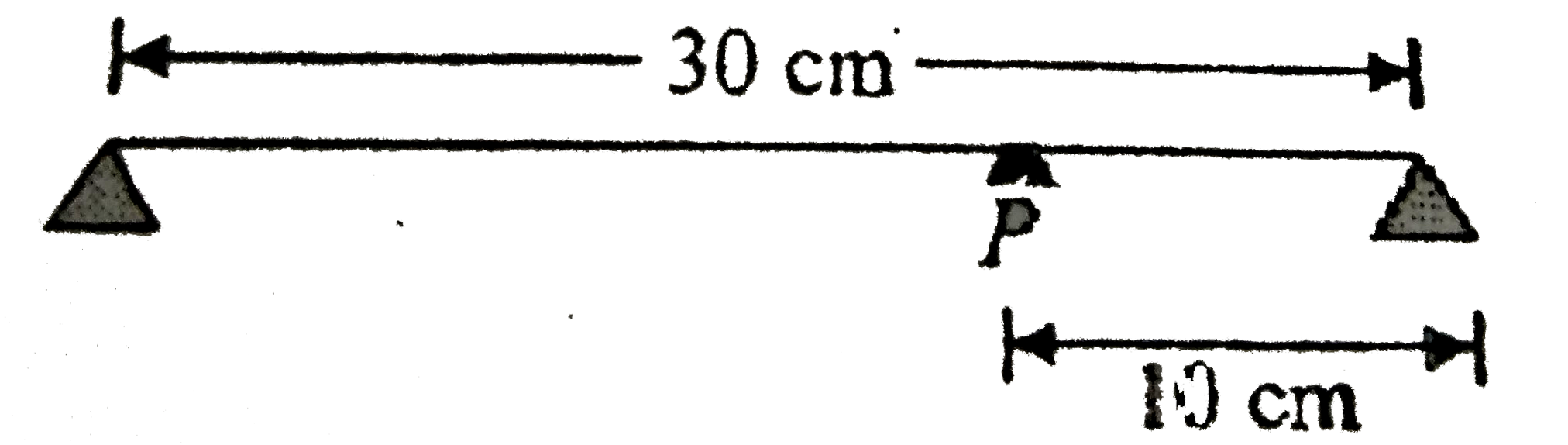
At which of the following frequencies the point P on string will have maximum oscillation amplitude among all points on string :
View SolutionFor the system shown in figure, the tensions in the string
View SolutionFind the tension in the strings AC and BC shown in figure.

View SolutionIn the following figure, if the tension in the string AB is 51N, then the tension in the string BC will be :-
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA uniform sphere of weight W and radius 5 cm is being held by string as shown in the figure. The tension in the string will be
View SolutionA uniform rod of mass 15kg is held stationary at 37 degree with the help of a light string as shown in Fig. The tension in the string is

View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
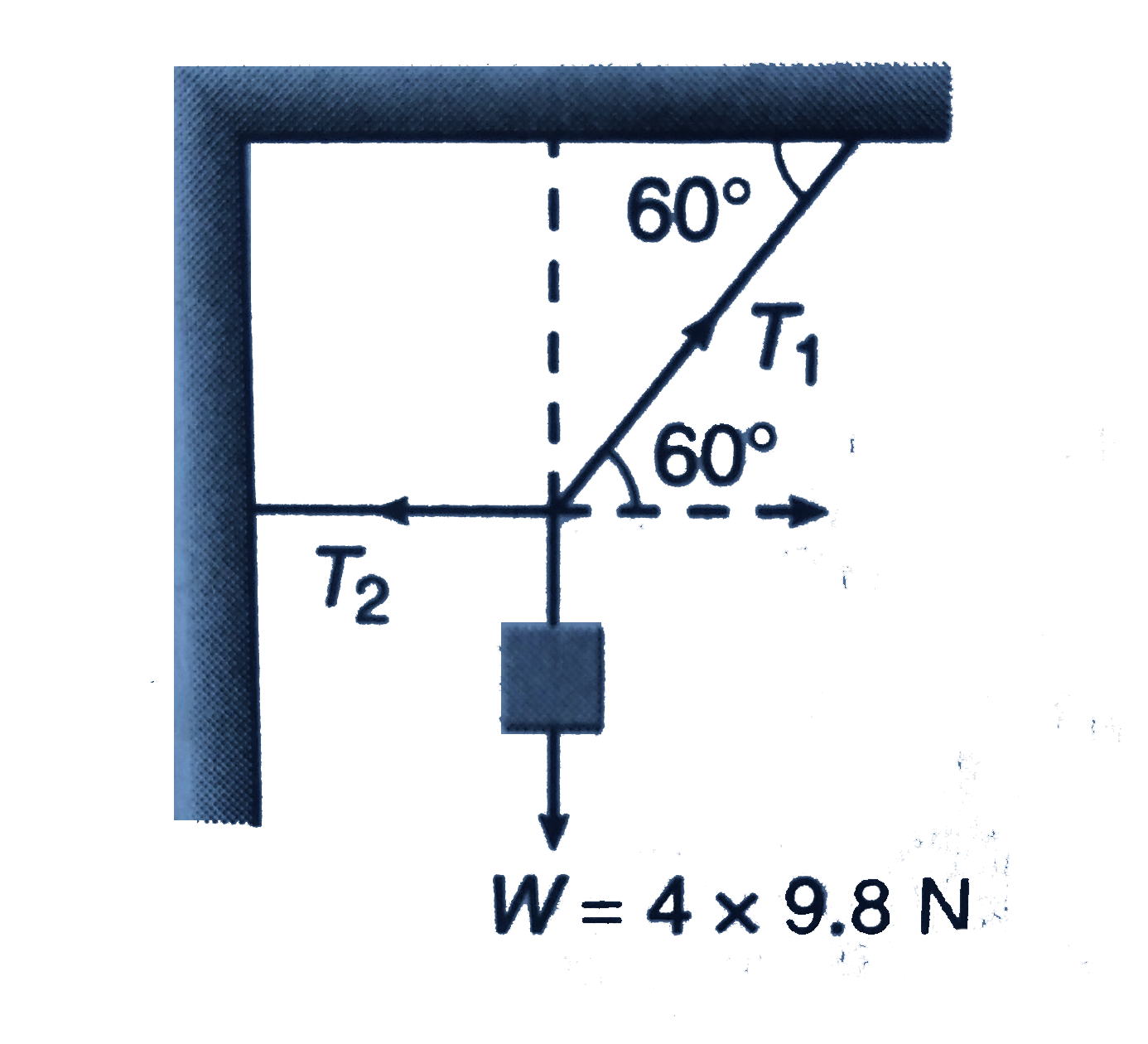
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.

View Solution
