A particle of positive charge q and mass m enters with velocity Vˆi at the origin in a magnetic field B(−ˆk) which is present in the whole space. The charge makes a perfectely inelastic collision with an identical particle (having same charge) ar rest but free to move at its maximum positive y-coordinate. After collision, the combined charge will move on trajectory where r=mVqB.
y=mvqB(−ˆi)
(x+r)2+(y−r/2)2=r2/4
(x−r)2+(y−r)2=r2
(x−r)2+(y+r/2)2=r2/4
The correct Answer is:B
To solve the problem step-by-step, we will analyze the motion of the charged particles in the magnetic field and the effects of the inelastic collision.
Step 1: Understand the Initial Motion of the Charged Particle
A particle with charge q and mass m enters the magnetic field with velocity →V=V^i at the origin. The magnetic field is given by →B=−B^k.
Hint: The force on a charged particle in a magnetic field is given by the Lorentz force →F=q(→V×→B).
Step 2: Calculate the Force Acting on the Particle
Using the cross product to find the direction of the force:
→F=q(→V×→B)=q(V^i×(−B^k))
Calculating the cross product:
^i×^k=^j(using the right-hand rule)
Thus,
→F=−qVB^j
This indicates that the force is acting in the negative y-direction.
Hint: The force acts perpendicular to the velocity, causing circular motion.
Step 3: Determine the Radius of the Circular Path
The radius R of the circular path of the charged particle in a magnetic field is given by:
R=mvqB
where v is the speed of the particle.
Hint: This formula arises from equating the centripetal force to the magnetic force.
Step 4: Analyze the Collision
The particle collides inelastically with another identical particle (charge q, mass m) that is at rest. After the collision, the two particles will move together with a combined mass of 2m and charge 2q.
Hint: In an inelastic collision, momentum is conserved.
Step 5: Apply Conservation of Momentum
Before the collision, the momentum of the moving particle is:
pinitial=mv
After the collision, the combined momentum is:
pfinal=(2m)v′
Setting the initial momentum equal to the final momentum:
mv=(2m)v′⟹v′=v2
Hint: The new velocity after the collision is half of the original velocity due to the doubling of mass.
Step 6: Calculate the New Radius After Collision
The new radius R′ of the circular path after the collision can be calculated using the new speed:
R′=(2m)(v/2)(2q)B=mvqB=R
However, since the momentum is now shared, the effective radius becomes:
R′=R2
Hint: The radius decreases because the effective charge moving in the field has doubled while the speed has halved.
Step 7: Determine the Center of the New Circular Path
The center of the new circular path will be at coordinates:
Center=(−R′,R′2)=(−R2,R4)
Hint: The center of the circle is determined by the radius and the direction of the motion.
Step 8: Write the Equation of the Circle
The general equation of a circle with center (a,b) and radius r is:
(x−a)2+(y−b)2=r2
Substituting the values:
(x+R2)2+(y−R4)2=(R2)2
Hint: This equation describes the trajectory of the combined charge after the collision.
Final Result
The trajectory of the combined charge after the collision can be represented by the equation:
(x+R2)2+(y−R4)2=R24
A particle with charge q and mass m enters the magnetic field with velocity →V=V^i at the origin. The magnetic field is given by →B=−B^k.
Using the cross product to find the direction of the force:
→F=q(→V×→B)=q(V^i×(−B^k))
Calculating the cross product:
^i×^k=^j(using the right-hand rule)
Thus,
→F=−qVB^j
This indicates that the force is acting in the negative y-direction.
The radius R of the circular path of the charged particle in a magnetic field is given by:
R=mvqB
where v is the speed of the particle.
The particle collides inelastically with another identical particle (charge q, mass m) that is at rest. After the collision, the two particles will move together with a combined mass of 2m and charge 2q.
Before the collision, the momentum of the moving particle is:
pinitial=mv
After the collision, the combined momentum is:
pfinal=(2m)v′
Setting the initial momentum equal to the final momentum:
mv=(2m)v′⟹v′=v2
The new radius R′ of the circular path after the collision can be calculated using the new speed:
R′=(2m)(v/2)(2q)B=mvqB=R
However, since the momentum is now shared, the effective radius becomes:
R′=R2
The center of the new circular path will be at coordinates:
Center=(−R′,R′2)=(−R2,R4)
The general equation of a circle with center (a,b) and radius r is:
(x−a)2+(y−b)2=r2
Substituting the values:
(x+R2)2+(y−R4)2=(R2)2
The trajectory of the combined charge after the collision can be represented by the equation:
(x+R2)2+(y−R4)2=R24
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.52
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.53
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.50
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionA charged particle of specific charge α moves with a velocity →v=v0ˆi in a magnetic field →B=B0√2(ˆj+ˆk). Then (specific charge=charge per unit mass)
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionA particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
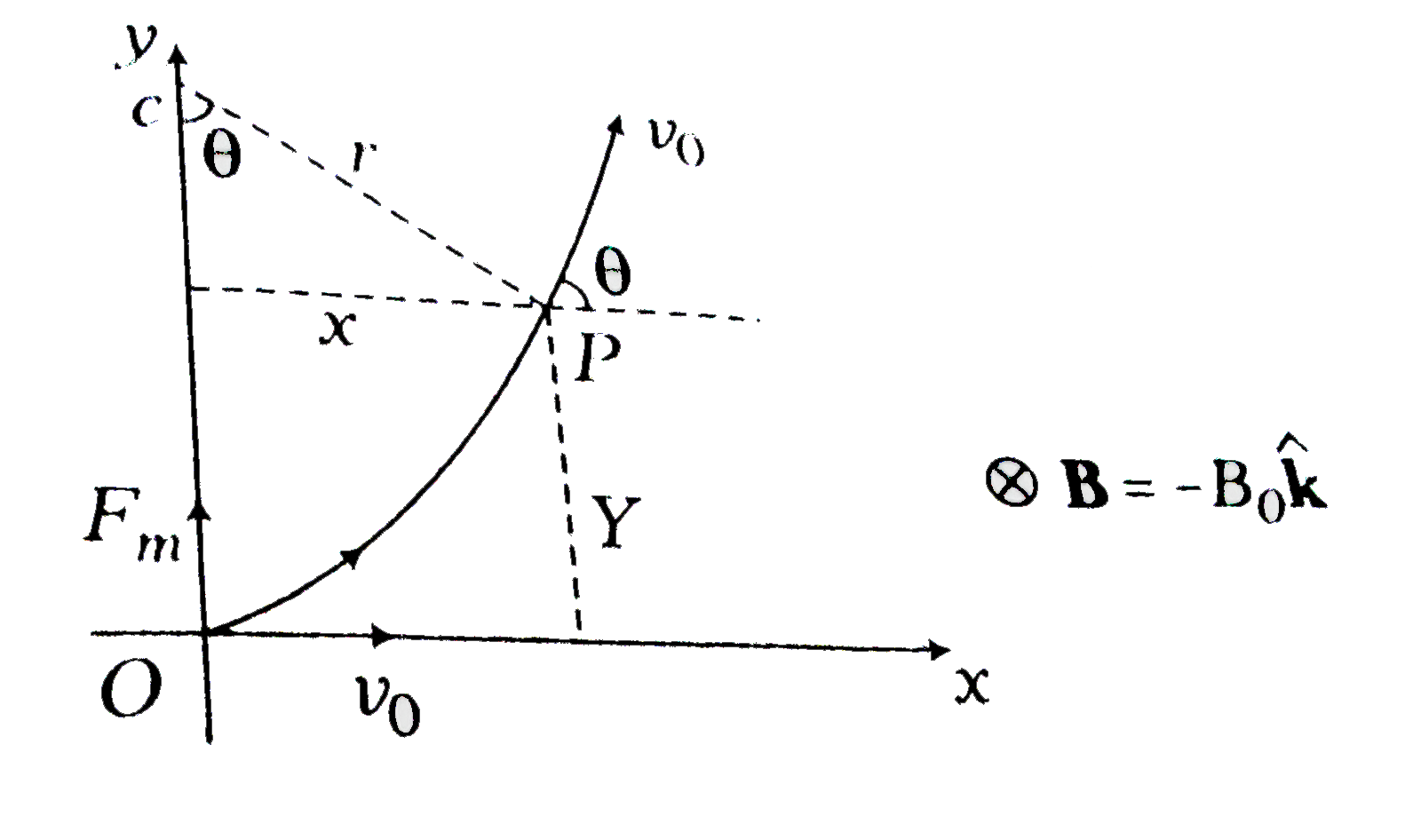
View SolutionA particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View Solution
