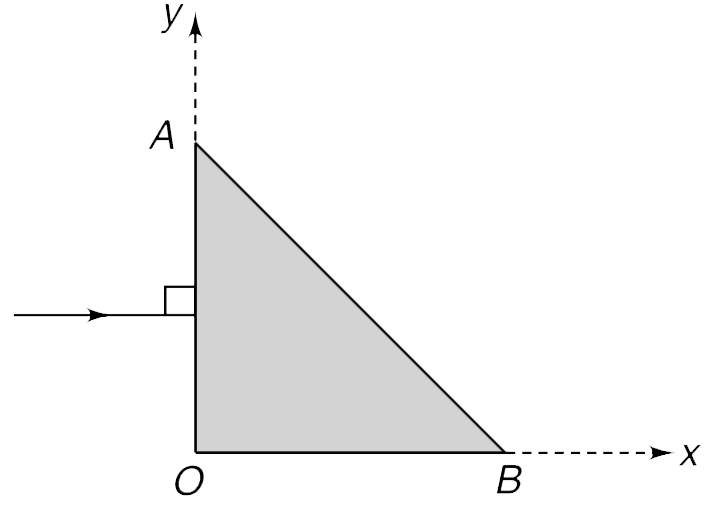
A triangular medium has varying refracting index μ=μ0+ax where x is the distance (in cm) along x-axis from origin and m0=4/3. A ray is incident normally on face OA at the mid-point of OA. Find the range of value of a so that light does not escape through face AB when it falls first time on the face AB.
a>19
a>29
a>13
None of these
The correct Answer is:B

Clearly PM=32cm
37∘>sin−11n0+a(3/2)
35>1n1+3a2⇒3n0+9a2>5
9a2>1⇒a>29.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.43
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.44
10 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.41
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
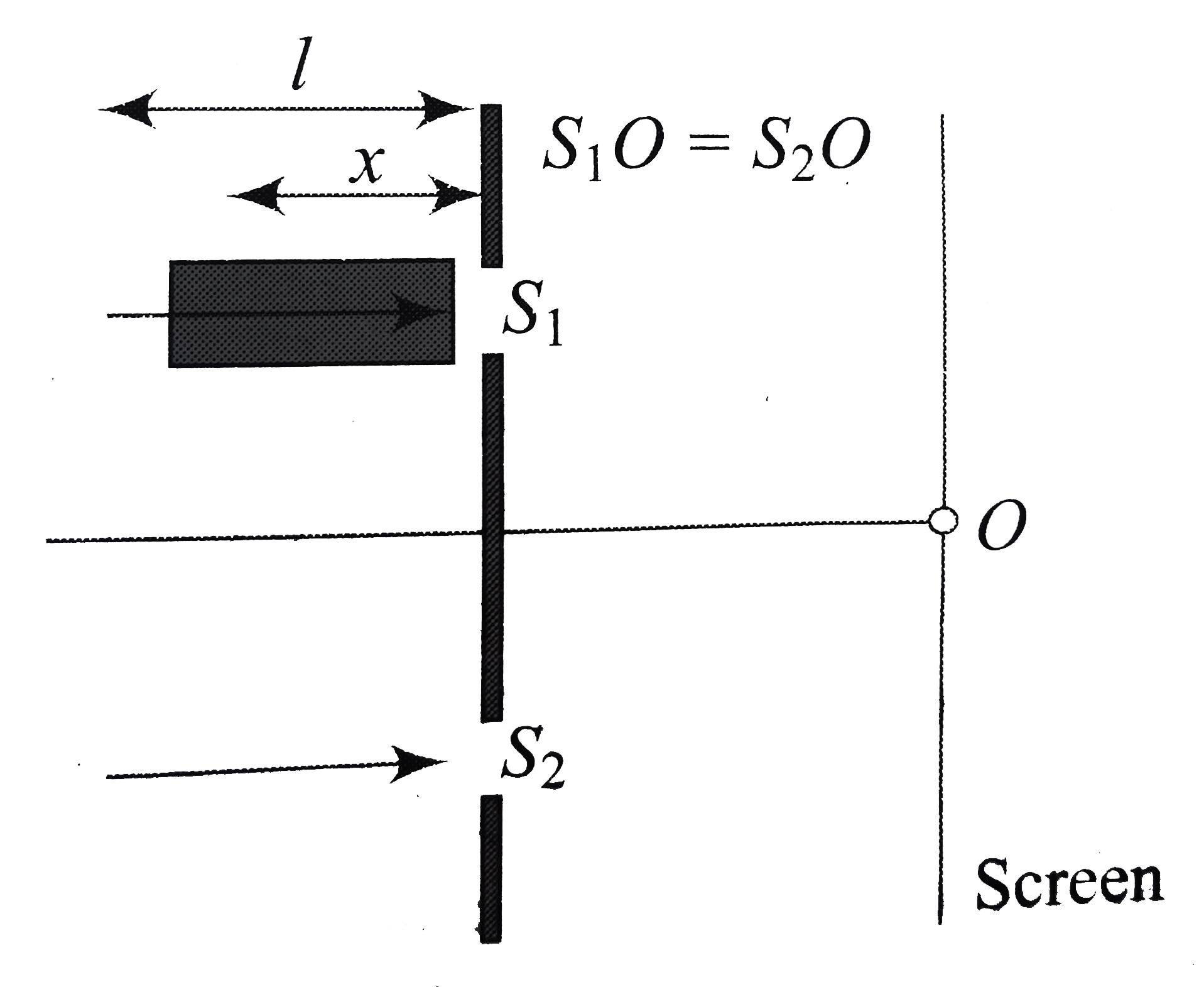
In figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit S1 passes through a medium of variable refractive index μ=1+ax (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on S1. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength λ in air) is
View SolutionA cylinderical glass rod of radius 0.1m and refractive index √3 lies on a horizontal plane mirror. A horizontal ray of light moving perpendicular to the axis of the rod is incident on it. At what height from the mirror should the ray be incident so that it leaves the rod at a height of 0.1m above the plane mirror? At what centre to centre distance a second similar rod, parallel to the first, be placed on the mirror, such that the emergent ray from the second rod is in line with the incident ray on the first rod?

View Solution
Knowledge Check
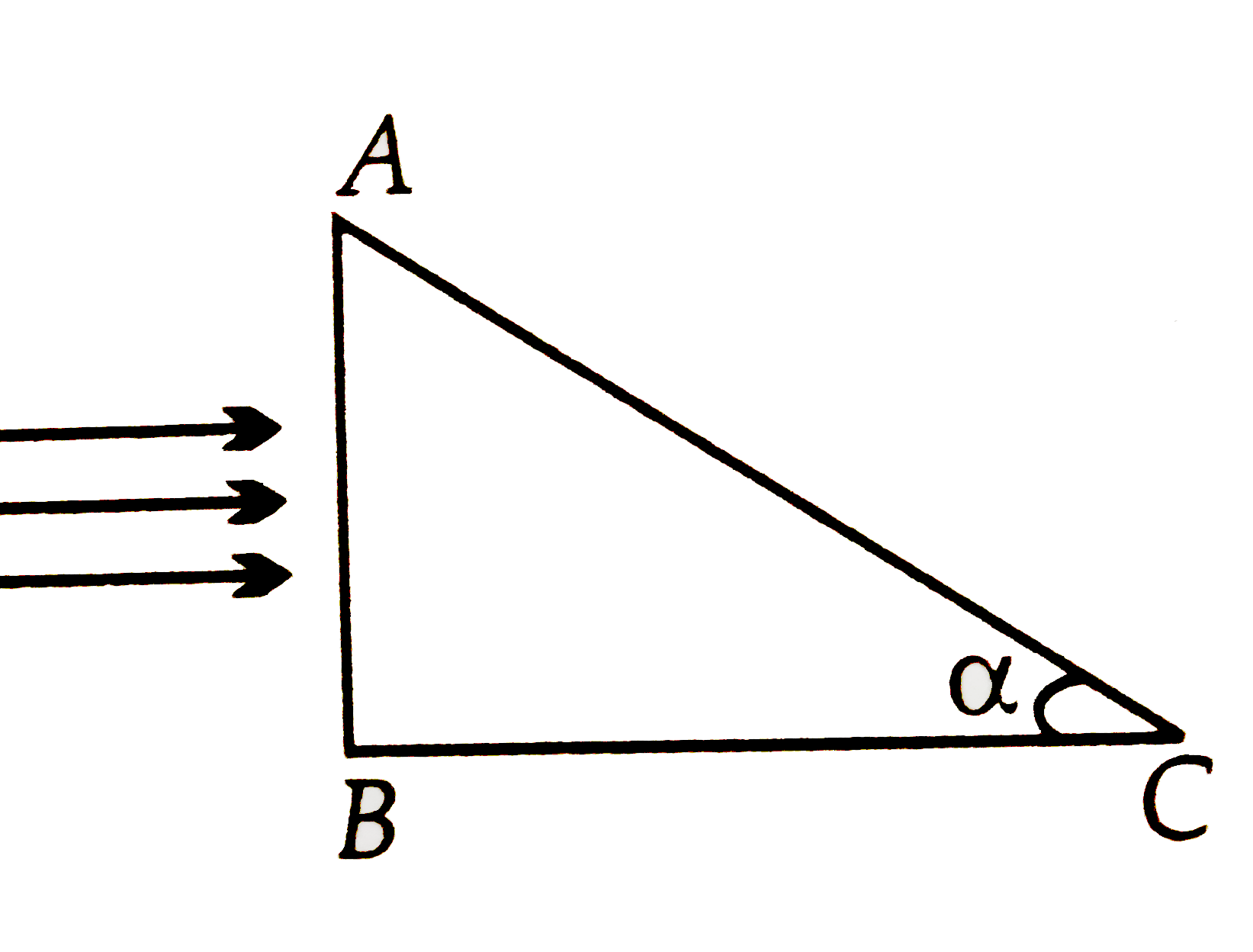
A ray of light is incident normally on the prism (μ=32) immersed in a liquid as shown in the figure. The largest value for the angle α so that ray is totally reflected at the face AC is 30∘. The refractive index of the given liquid is
 A√32B34C43D3√34
A√32B34C43D3√34
A biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View SolutionA system of coordinatees is drawn in a medium whose refractive index vaires as μ=21+Y2 where 0≤y≤1. A ray of light is incident at origin at an angle 60∘ with y-axis as shown in figure. At point P, the ray becomes parallel to x-axis, the volue of H is -

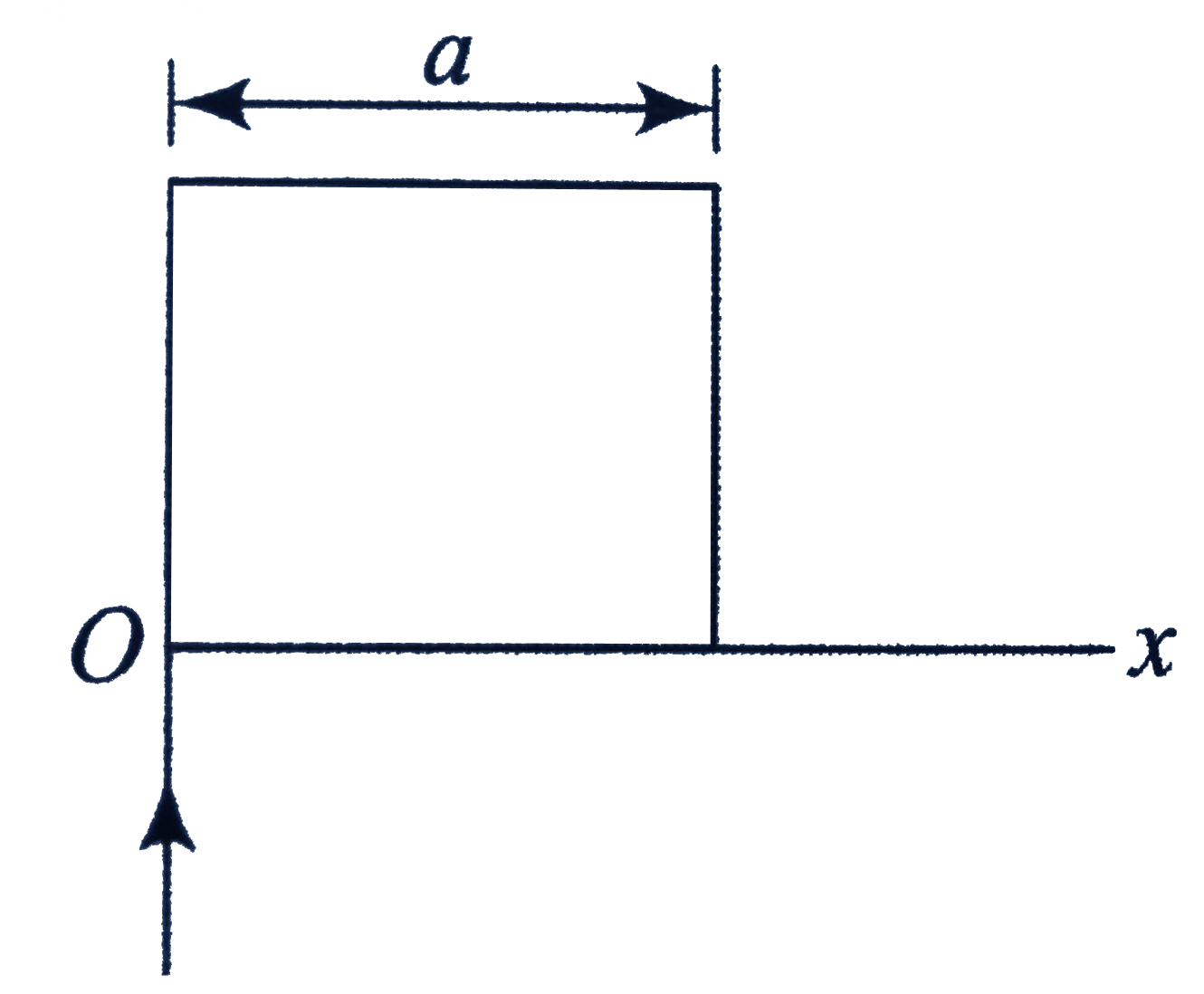
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View SolutionIn the given figure, the faces of prism ABCD made of glass with a refractive index n form dihedral angles ∠A=90∘,∠B75∘,,∠C=135∘&∠D=60∘ (The Abbe's prism) .A beam of light falls on face AB & after total internal reflection from face BC escapes through face AD.Find the range of n and angle of incidence α of the beam onto face AB, if a beam that has passed through the prism in this mahner is perpedicular to the incident beam.
View Solutionx-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View SolutionThe redius of curvature of the convex face of a plano-convex lens is 12cm and its refractive index is 1.5.
a. Find the focal length of this lens. The plane surface of the lens is now silvered.
b. At what distance form the lans will parallel rays incident on the convex face converge?
c. Sketch the ray diagram to locate the image, when a point object is places on the axis 20cm from the lens.
d. Calculate the image distance when the object is placed as in (c).
View SolutionA parallel beam of light falls on the surface of a convex lens whose radius of curvature of both sides of 20cm. The refractive index of the material of the lens varies as μ=1.5+0.5r , where r is the distance of the point on the aperture from the optical centre in cm. Find the length of the region on the axis of the lens where the light will appear. The radius of aperture of the lens is 1cm.
View Solution
