A particle P is moving on a circle under the action of only one force acting always fixed point O on the circumference . Find ratio of d2ϕdt2and(dϕdt)

The correct Answer is:2
a1=Fmsinθ⇒Rd2(2θ)dt2=Fmsinθ
d2θdt2=Fsinθ2mR ....(1)
ac=Fmcosθ,R[ddt(2θ)]2=Fmcosθ....(ii)
(d2θdt2)(dθdt)2=2tanθ=2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.42
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.43
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.40
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionA particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
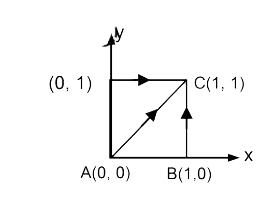
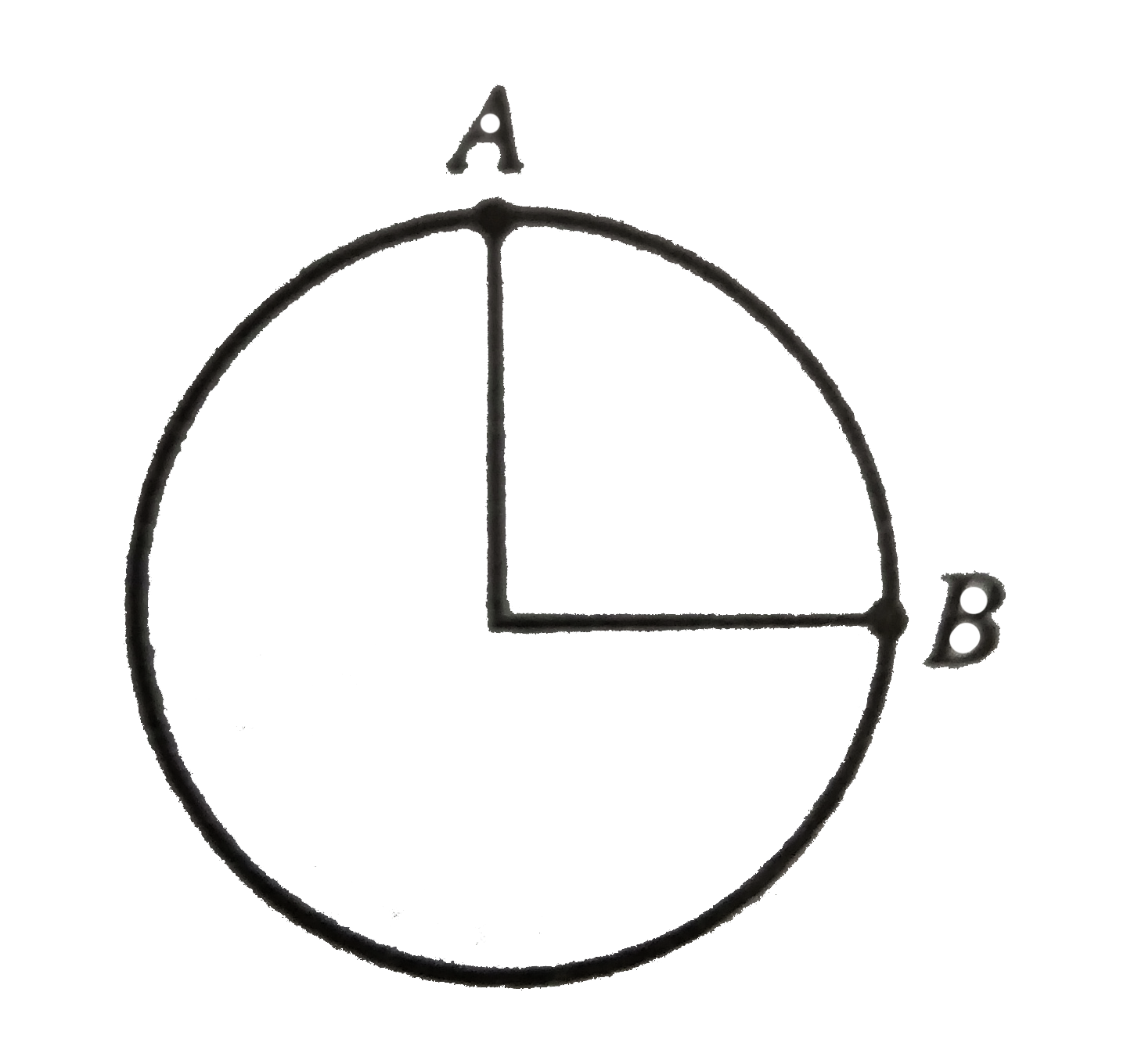
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
View Solutiony=Asinωt where A and ω are constants. Find d2ydt2.
View SolutionThe position of a particle moving on a stringht line under rthe action of a force is given as x=50t−5t2 Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is.
View SolutionThe ratio of the area and circumference of a circle of diameter d is
(a)d
(b) d2
(c)d4
(d) 2 d
View SolutionA particle has a time period of 1s under the action of a certain force and 2 s under the action of another force. Find the time period when the forces are acting in the same direction simultaneously.
View SolutionA particle moves from point (ˆi+ˆj)m to a point (6ˆi−2ˆj)m under the action of force (10ˆi−2ˆj)N. The work done by the force is
View SolutionThe ratio of the perimeter (circumference) and diameter of a circle is
(a)π
(b) 2π
(c)π2
(d) π4
View Solution

