A particle has a time period of 1s under the action of a certain force and 2 s under the action of another force. Find the time period when the forces are acting in the same direction simultaneously.
To solve the problem, we need to find the time period of a particle when two forces are acting on it simultaneously. The time periods under the action of each force are given as 1 second and 2 seconds.
1. Understand the Problem:
- We have two forces acting on a particle, with time periods T1=1s and T2=2s.
- We need to find the new time period Tnet when both forces act simultaneously.
2. Use the Relationship Between Time Period and Angular Frequency:
- The angular frequency ω is related to the time period T by the formula:
ω=2πT
- Therefore, for the two forces, we have:
ω1=2πT1=2π1=2πrad/s
ω2=2πT2=2π2=πrad/s
3. Calculate the Net Angular Frequency:
- When both forces act simultaneously, the net angular frequency ωnet can be calculated using the formula:
ω2net=ω21+ω22
- Plugging in the values:
ω2net=(2π)2+(π)2=4π2+π2=5π2
- Therefore:
ωnet=√5π2=π√5
4. Find the New Time Period:
- Now, we can find the new time period Tnet using the relationship between angular frequency and time period:
Tnet=2πωnet
- Substituting the value of ωnet:
Tnet=2ππ√5=2√5s
Final Answer:
The time period when both forces act simultaneously is:
Tnet=2√5s
- We have two forces acting on a particle, with time periods T1=1s and T2=2s.
- We need to find the new time period Tnet when both forces act simultaneously.
- The angular frequency ω is related to the time period T by the formula:
ω=2πT
- Therefore, for the two forces, we have:
ω1=2πT1=2π1=2πrad/s
ω2=2πT2=2π2=πrad/s
- When both forces act simultaneously, the net angular frequency ωnet can be calculated using the formula:
ω2net=ω21+ω22
- Plugging in the values:
ω2net=(2π)2+(π)2=4π2+π2=5π2
- Therefore:
ωnet=√5π2=π√5
- Now, we can find the new time period Tnet using the relationship between angular frequency and time period:
Tnet=2πωnet
- Substituting the value of ωnet:
Tnet=2ππ√5=2√5s
The time period when both forces act simultaneously is:
Tnet=2√5s
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL SOLVED PROBLEMS
11 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS WITH ANSWER
20 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
A body has a time of 3 s under the action of one force and 4 s under the action of another force. Calculate the time period when both the forces act in the same direction simultaneously. Assume that the body undergoes the same displacement, under the action of the two different forces.
View SolutionA particle under the action of one SHM has a period of 3 s and under the effect of another it has a period 4s. Its time period under the combined action of both the SHM's in the same direction is (0.4x)second. Find value of x?
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA particle under the action of a force has a period of 3s and under the action of another force it has a period 4sec in SHM. What will be its period under the combined action of both forces in the same direction?
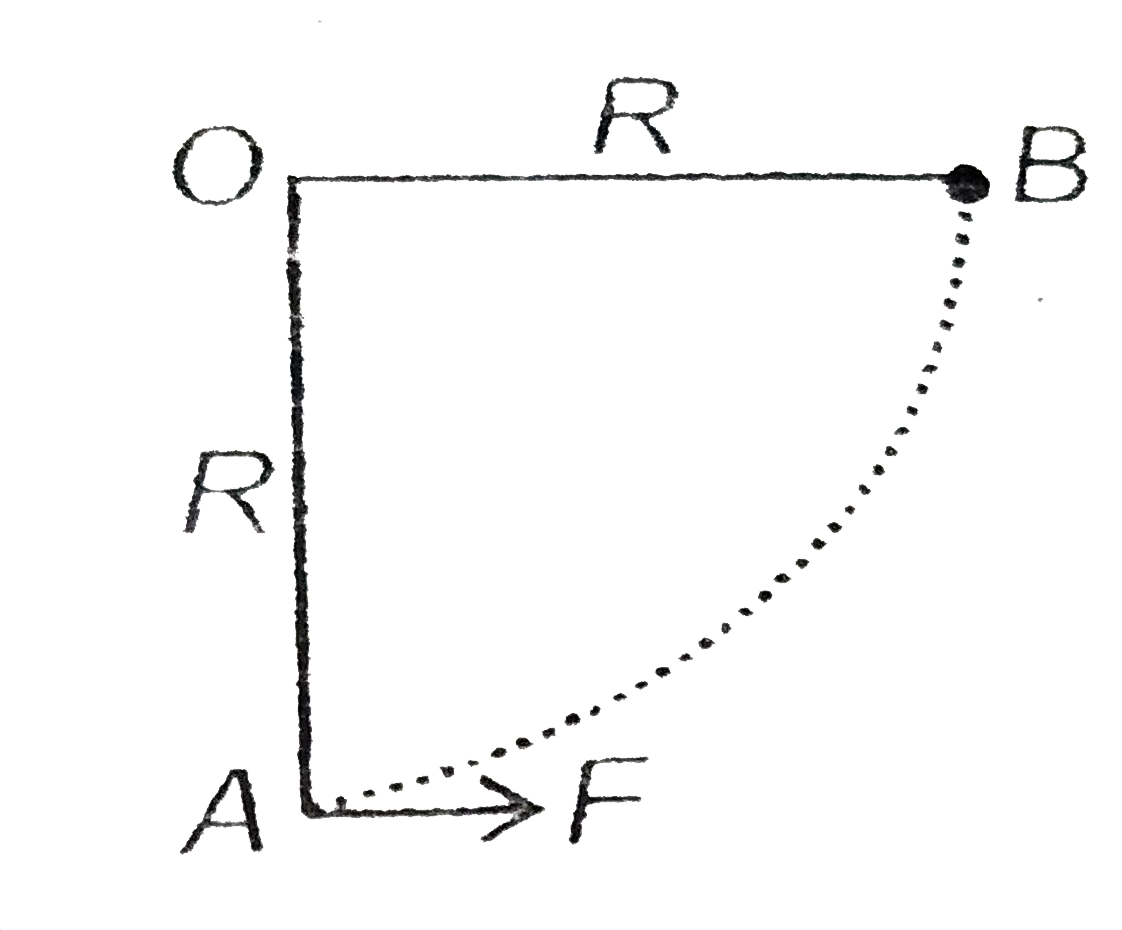
View SolutionA block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA body executes SHM under the influence of one force and has a period T1 seconds and the same body executes SHM with period T2 seconds when under the influence of another force. When both forces act simultaneously and in the same direction, then the time period of the same body (in seconds) is:
View SolutionUnder the action of a constant force, A particle is experiencing a constant acceleration. The power is
View SolutionA particle starts its motion from rest under the action of a constant force. If the distance covered in first 10s is s1 and the covered in the first 20s is s2, then.
View SolutionA body is moving with an acceleration 'a' under the action of a force 'g'. The weight of the body is
View Solution
