Question

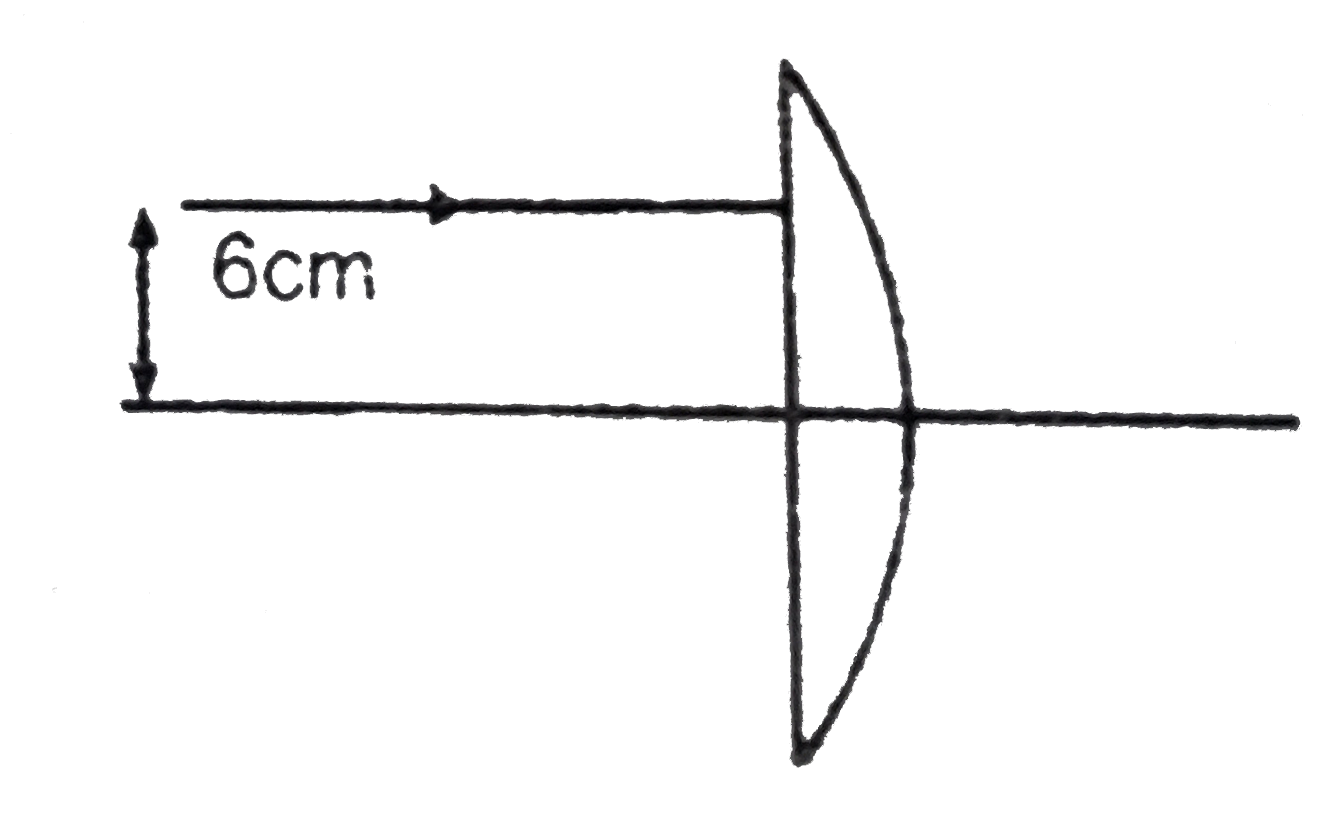
A light ray parallel to the principal axis is incident (as shown in the figure) on a thin planoconvex lens with radius of curvature of its curved part equal to 10 cm. Assuming that the refractive index of the material of the lens is ${\displaystyle 4/3}$ and medium on both sides of the lens is air, find the distance of the point from the lens where this ray meets the principal axis. Find your answer in the form ${\displaystyle \frac{X}{7}cm}$ and fill value of ${\displaystyle X}$ .

Answer

A::C

Explanation

`R = 10 cm`

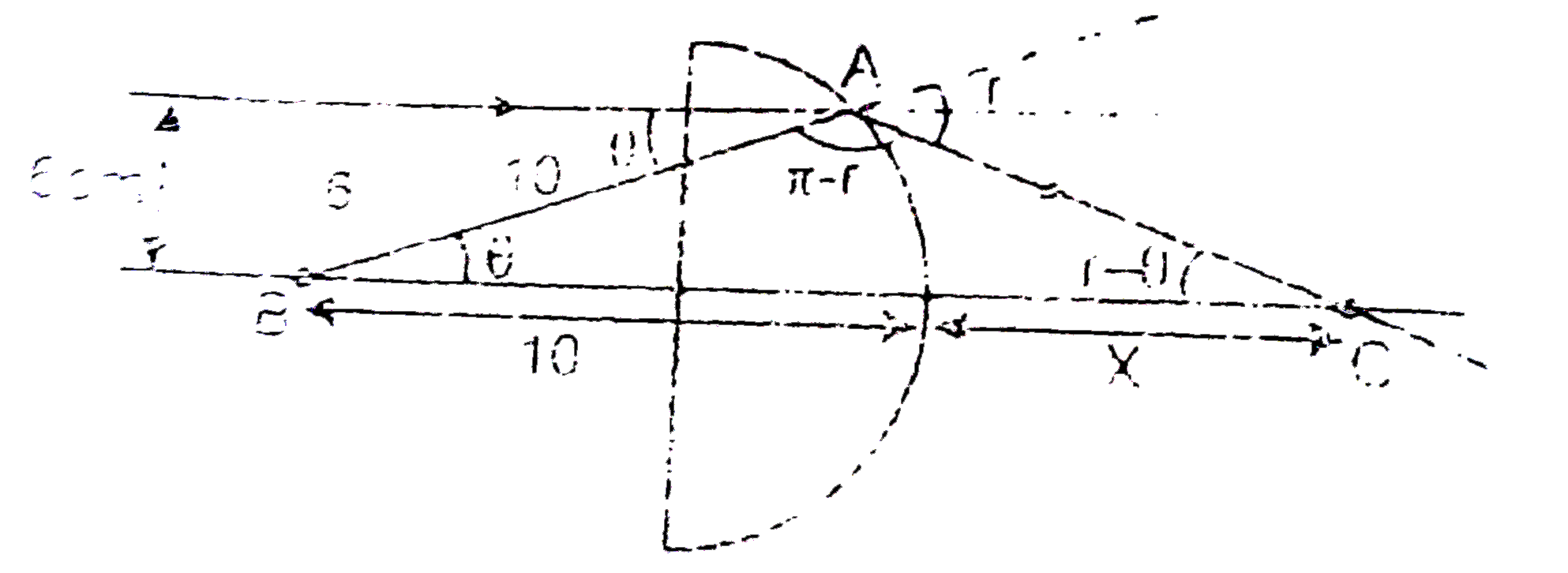
Applying snell's law `(sin theta)/(sin r) = (3)/(4) rArr r = 53^(@)`
By sine law in `Delta ABC (sin r = 0)/(10) = (sin(pi -r))/((10+x))`
`(10 -x)/(10)=(4)/(5(sin r cos theta - cos r sin theta))`
`=(4)/(5((4)/(5)xx(4)/(5)-(3)/(5) xx(3)/(5)))=10 + x= (200)/(7)`
`rArr x = (200 -70)/(7) = (130)/(7)`.