A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.

Time taken to cover the distance in above part is :
(√2+14√2)sec
(√2−14√2)sec
14√2sec
18sec
The correct Answer is:C
t=xvA=14√2sec
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.21
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.22
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.19
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.
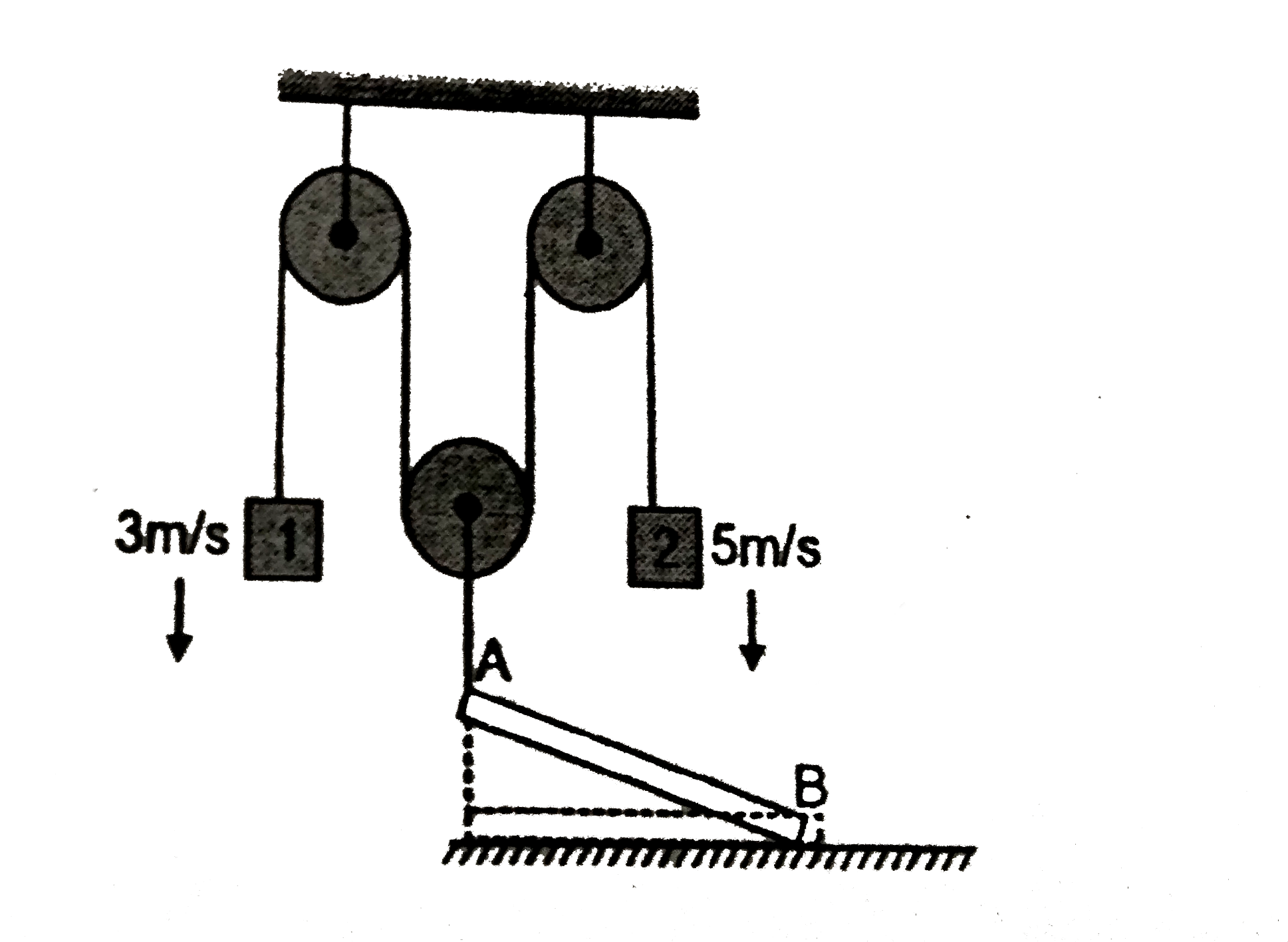
Minimum magnitude of relative velocity of A with respect to B during the motino specified in question 5 is :
View SolutionA meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.
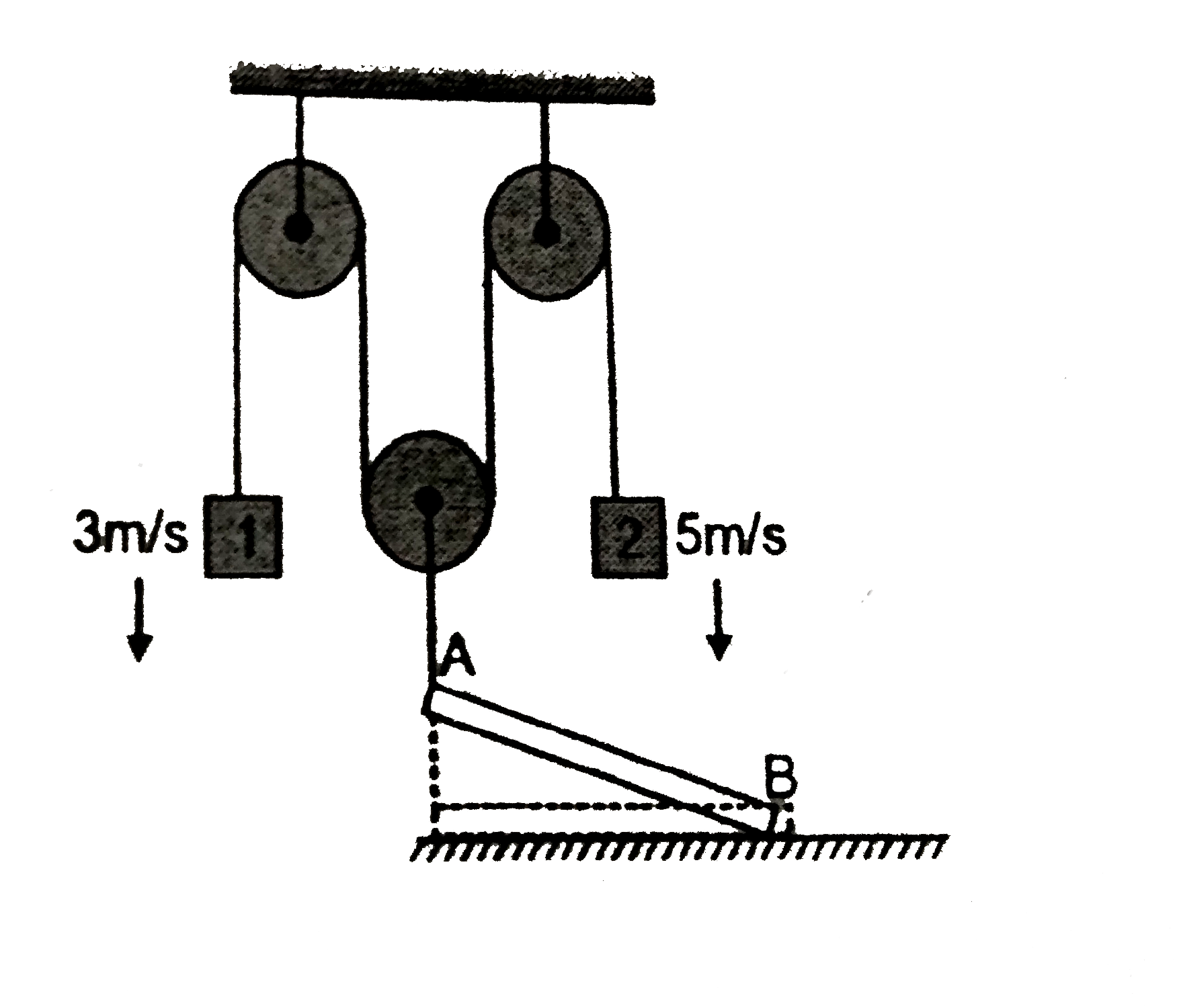
If block 1 and 2 are given constant speeds as shown then the distance moved by end B over the floor in the period for which speed of B is less than A.
View Solution
Knowledge Check
Two identical small masses each of mass m are connected by a light inextensible string on a smooth horizontal floor. A constant force F is applied at the mid point of the string as shown in fig. find the acceleration of each mass towards each other.
 AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.

If block 1 and 2 are given constant speeds as shown then the distance moved by end B over the floor in the period for which speed of B is less than A.
View SolutionTwo identical blocks are attached by a massless string running over a pulley as shown in figure. The rope initially runs over the pulley at its (the rope's) midpoint, and the surface that block 1 rests on is frictionless. Blocks 1 and 2 are initially at rest when block 2 is released with the string taut and horizontal. Assume that the initial distance from block 1 to the pulley is the same as the initial distance from block 2 to the wall.
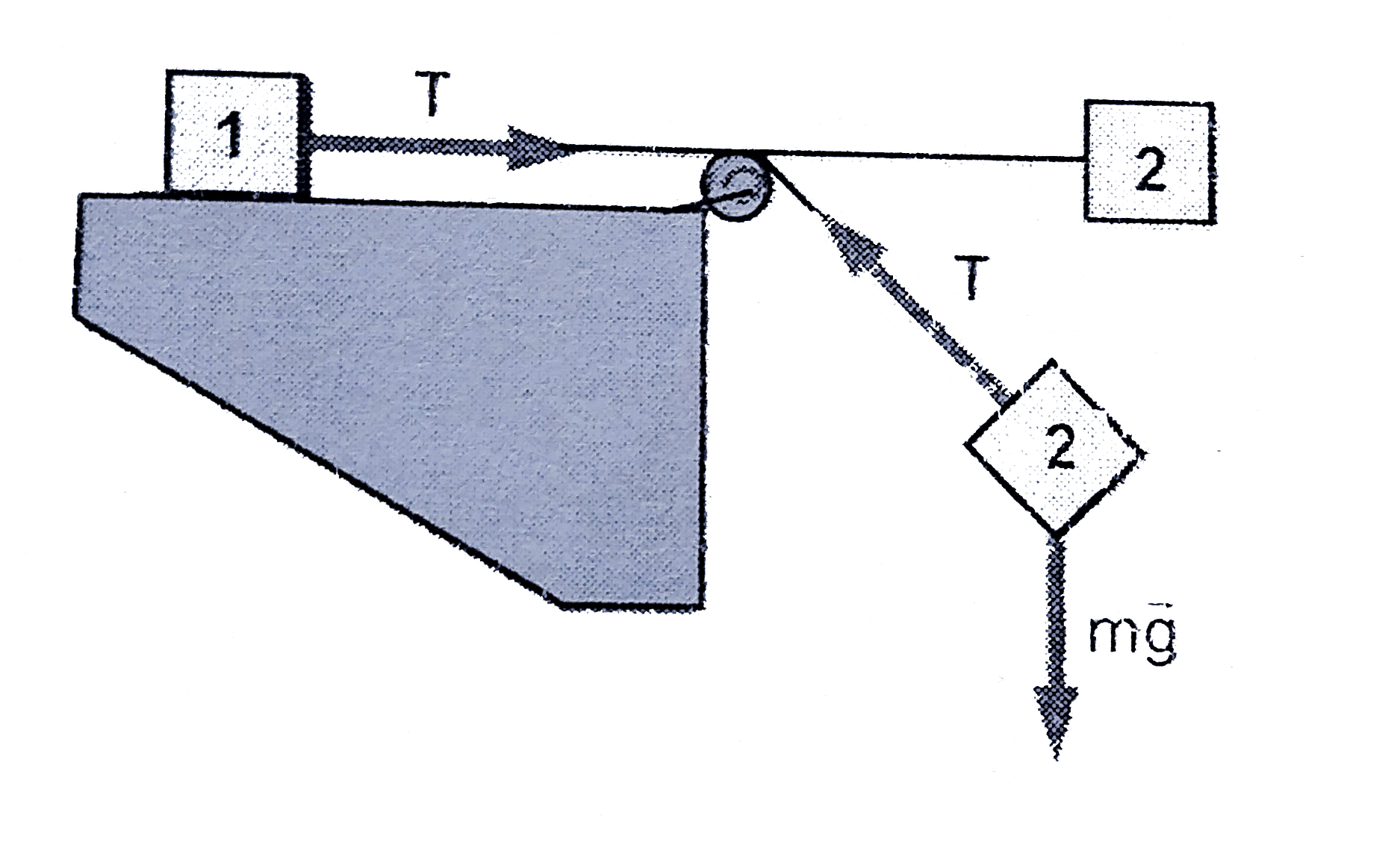
View Solution
Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling . The rod is of mass 'm' and has another weight of mass 2 m hung at a distance of 75 cm from A . The tension in the string at A is :
View SolutionA light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)
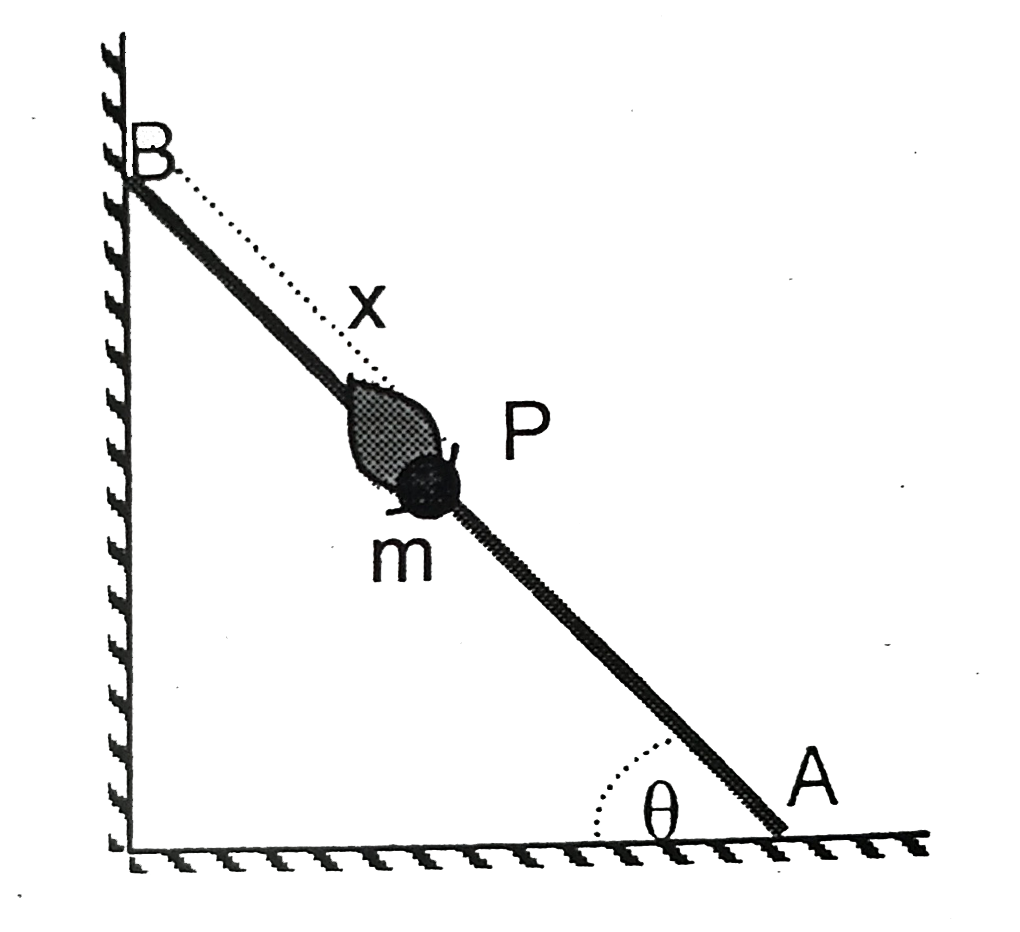
View SolutionThere blocks a,b and c of massses 10 kg ,10 kg and 20 kg respectivaly are arrenged as shown in figure all the surface are frictionless and string is inextensible A constant force F= 20N is applied on block a as shown . pulley and string are light . part of the string connecting both pulleys is vertical and part of the string connecting pulleys with masses a and b are horizontal .
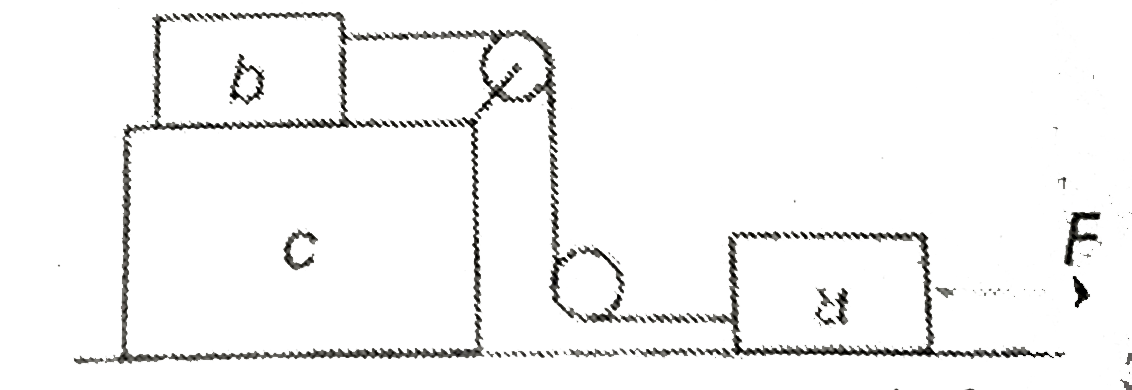
View SolutionA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
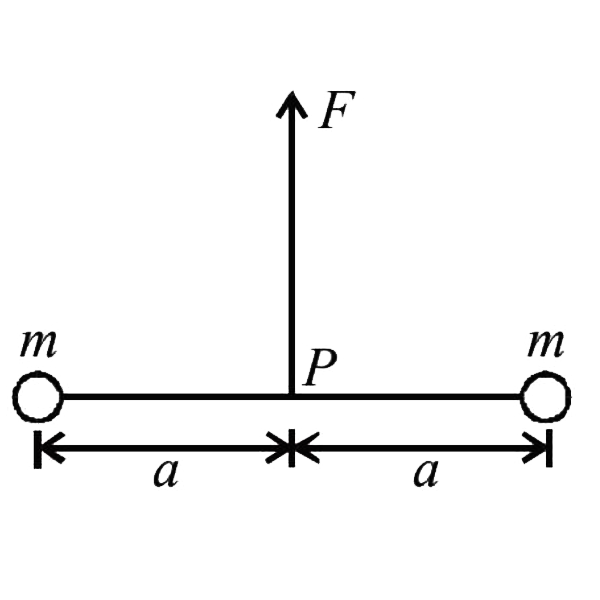
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View Solution
