The radius of the orbit of an electron in Hydrogen-like aton is 4.5 α0 where α0 is the Bohr radius. Its orbital angular momentum is 3h2π. It is given that h is Planck's constant and R is Rydberg constant. The possible wavelength (s), when the atom de-excites, is (are)
932R
916R
95R
93R
The correct Answer is:A, C
Rn=4.5a0
L=mvr=3h2π[asn=3,x=2]
1λ=Rz2⎛⎝1n2f−1n21⎞⎠
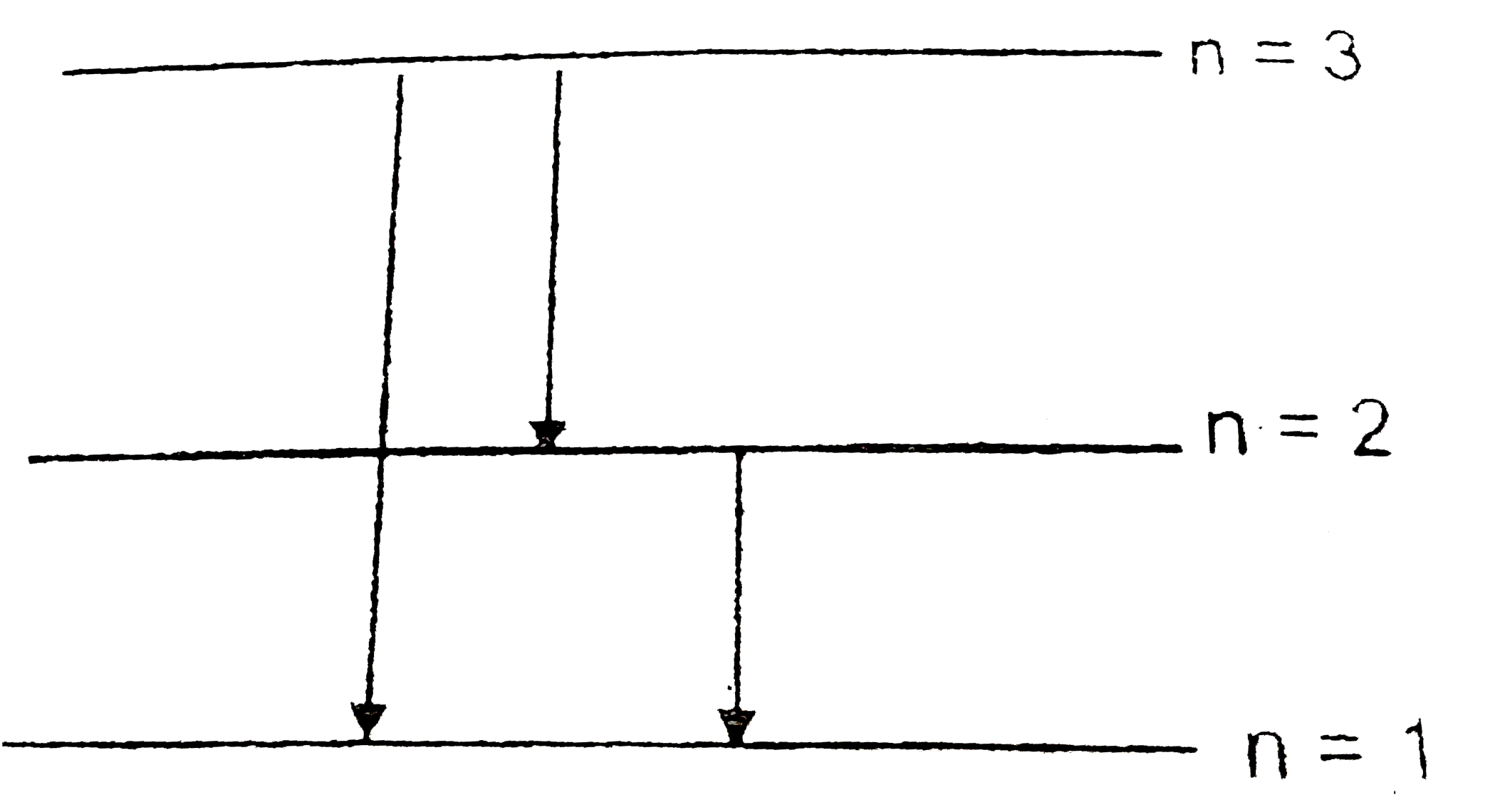
1λ3→1R4[11−19]=4R89⇒λ3→1=932R
1λ2→1=R4[11−14]=344R⇒λ2→1=13R
1λ3→2=R4[14−19]=5364R⇒λ3→2=95R.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.21
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.22
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.19
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
The radius of the orbit of an electron in a Hydrogen - like atom is 4.5s0 where a0 is the bohr radius its orbital angular momentum is 3h2π it is given that is is plank constant and R is rydberg constant .The possible wavelength (s) , when the atom de- excite , is (are)
View SolutionWhen a hydrogen atoms emits a photon of energy 12.1eV , its orbital angular momentum changes by (where h os Planck's constant)
View Solution
Knowledge Check
The radius of nth orbit rn in the terms of Bohr radius (a0) for a hydrogen atom is given by the relation
Ana0B√na0Cn2a0Dn3a0
The radius of the first Bohr orbit of hydrogen atom is 0.529Å. The radius of the third orbit of H will be:
View SolutionThe energy of an excited hydrogen atom is 0.38 eV. Its angular momentum is n.h2π . Find n
View SolutionIn an e− transition inside a hydrogen atom, orbital angular momentum may change by (h=Planck's constant)
View SolutionThe angular momentum J of the electron in a hydrogen atom is proportional to nth power of r (radius of the orbit) where n is :-
View SolutionWhen an electron in hydrogen atom is excited, from its 4th to 5th stationary orbit, the change in angular momentum of electron is (Planck's constant: h=6.6×10−34J−s)
View Solutionde-Broglie wavelength of electron in 2nd excited state of hydrogen atom is: [where r0 is the radius of 1st orbit in H-atom]
View SolutionThe angular momentum of an electron in the hydrogen atom is 3h2π Here. h is Planck's constant. The kinetic energy of this electron is
View Solution
