An object lies in front if a thick parallel glass slab, the bottom of which is published if the distance between m first two images formed by bottom surface is then find the thickness of the slab [Assume paraxial rays].
a.2 cm
b.4 cm
c.6 cm
d.none of these
The correct Answer is:A
To solve the problem, we need to determine the thickness of the glass slab based on the given information about the images formed by the bottom surface. Let's break down the solution step by step.
1. Understanding the Setup:
- We have a thick parallel glass slab with a polished bottom surface.
- An object is placed in front of the slab, and the refractive index of the glass is given as n=32.
- The distance between the first two images formed by the bottom surface of the slab is given as 4cm.
2. Apparent Distance Calculation:
- When light rays pass through the glass slab, they bend due to refraction. The apparent distance of the object from the top surface of the slab can be calculated using the formula:
X′=Xn
where X is the actual distance of the object from the top surface and n is the refractive index of the glass.
3. Total Distance to the Bottom Surface:
- The total distance from the bottom surface of the slab to the object is:
Distance to bottom=X′+T=Xn+T
where T is the thickness of the slab.
4. Finding the First Image:
- The first image formed by the bottom surface of the slab is at the same distance from the bottom surface as the apparent distance calculated above:
First Image Position=Xn+T
5. Finding the Second Image:
- The second image will be formed at a distance of Xn+2T from the bottom surface, as it reflects back after passing through the slab.
6. Distance Between the Two Images:
- The distance between the first and second images is given as 4cm:
(Xn+2T)−(Xn+T)=4cm
- Simplifying this gives:
2T−T=4cm⟹T=4cm
7. Final Calculation:
- From the above equation, we find:
T=2cm
Conclusion:
The thickness of the slab T is 2cm.
- We have a thick parallel glass slab with a polished bottom surface.
- An object is placed in front of the slab, and the refractive index of the glass is given as n=32.
- The distance between the first two images formed by the bottom surface of the slab is given as 4cm.
- When light rays pass through the glass slab, they bend due to refraction. The apparent distance of the object from the top surface of the slab can be calculated using the formula:
X′=Xn
where X is the actual distance of the object from the top surface and n is the refractive index of the glass.
- The total distance from the bottom surface of the slab to the object is:
Distance to bottom=X′+T=Xn+T
where T is the thickness of the slab.
- The first image formed by the bottom surface of the slab is at the same distance from the bottom surface as the apparent distance calculated above:
First Image Position=Xn+T
- The second image will be formed at a distance of Xn+2T from the bottom surface, as it reflects back after passing through the slab.
- The distance between the first and second images is given as 4cm:
(Xn+2T)−(Xn+T)=4cm
- Simplifying this gives:
2T−T=4cm⟹T=4cm
- From the above equation, we find:
T=2cm
The thickness of the slab T is 2cm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.10
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.11
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.8
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A point object is placed at a distance of 20 cm from a glass slab, H=18cm, half immersed in water as shown in figure. The distance between two images when seen from the other side of the slab is (μg=32andμw=43)
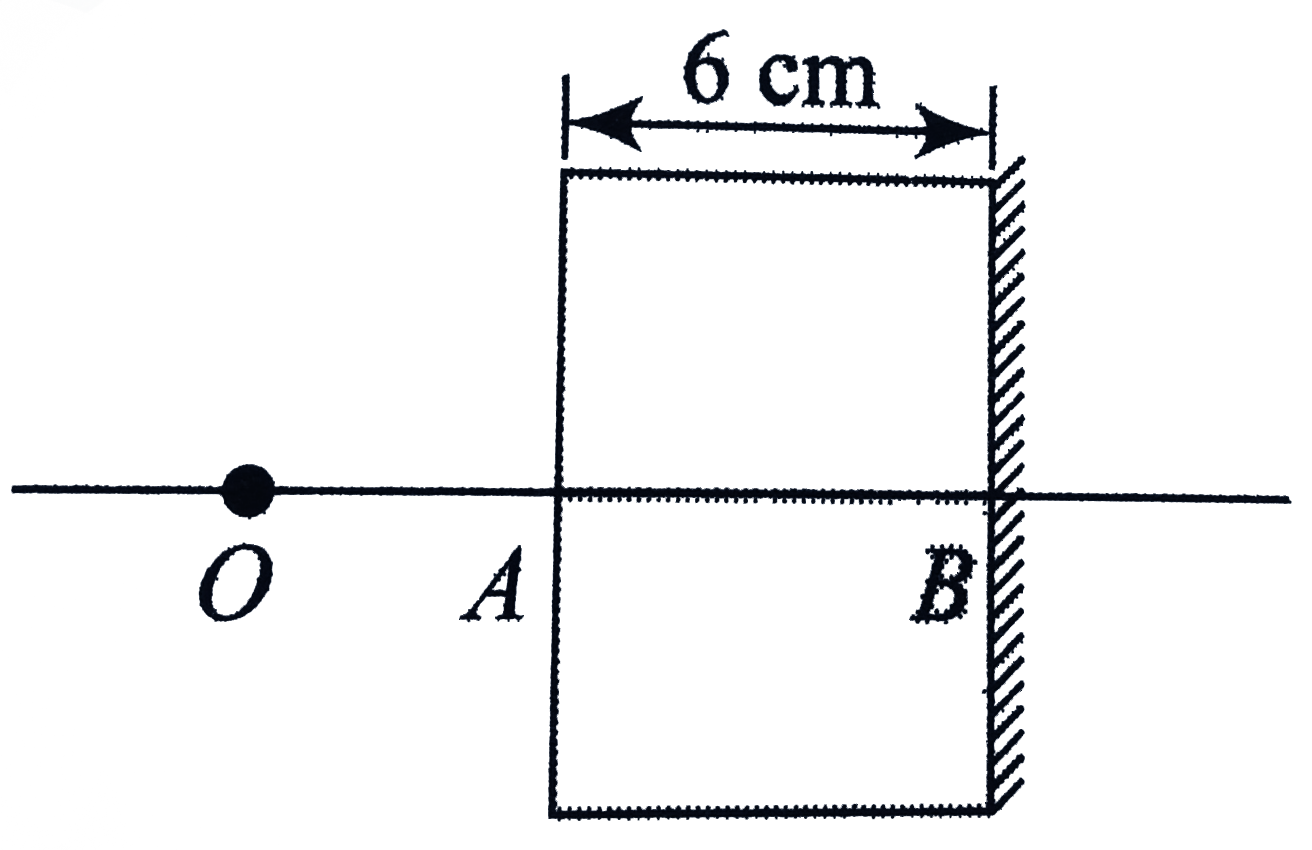
View SolutionAn object O is placed at 8cm in front of a glass slab, whose one face is silvered as shown in Figure. The thickness of the slab is 6cm. If the image formed 10 cm behind the silvered face, find the refractive index of glass.
View SolutionA small object is placed 20 cm in front of a block of glass 10 cm thick and its farther side silvered. The image is formed 22 cm behind the silvered face. Find the refractive index of glass.
View SolutionA point object is placed at a distance of 25cm from a convex lens. Its focal length is 22cm. A glass slab of refractive index 1.5 is inserted between the lens and the object, then the image is formed at infinity. Find the thickness of the glass slab (in cm).
View SolutionOnc face of a rectangular glass plate 6 cm thick is silcerd. An object held 8 cm in front of the first face, froms an image 12 cm behind the silvered face. The refractive index of the glass is
View SolutionOne face of a rectangular glass plate 6 cm thick is silvered. An object held 8 cm in front of the first face, forms an image 12 cm behind the silvered face. The refractive index of the glass is
View SolutionOne face of a rectangular glass plate 6 cm thick is silvered. An object held 8 cm in front of the first face, forms an image 12 cm behind the silvered face. The refractive index of the glass is
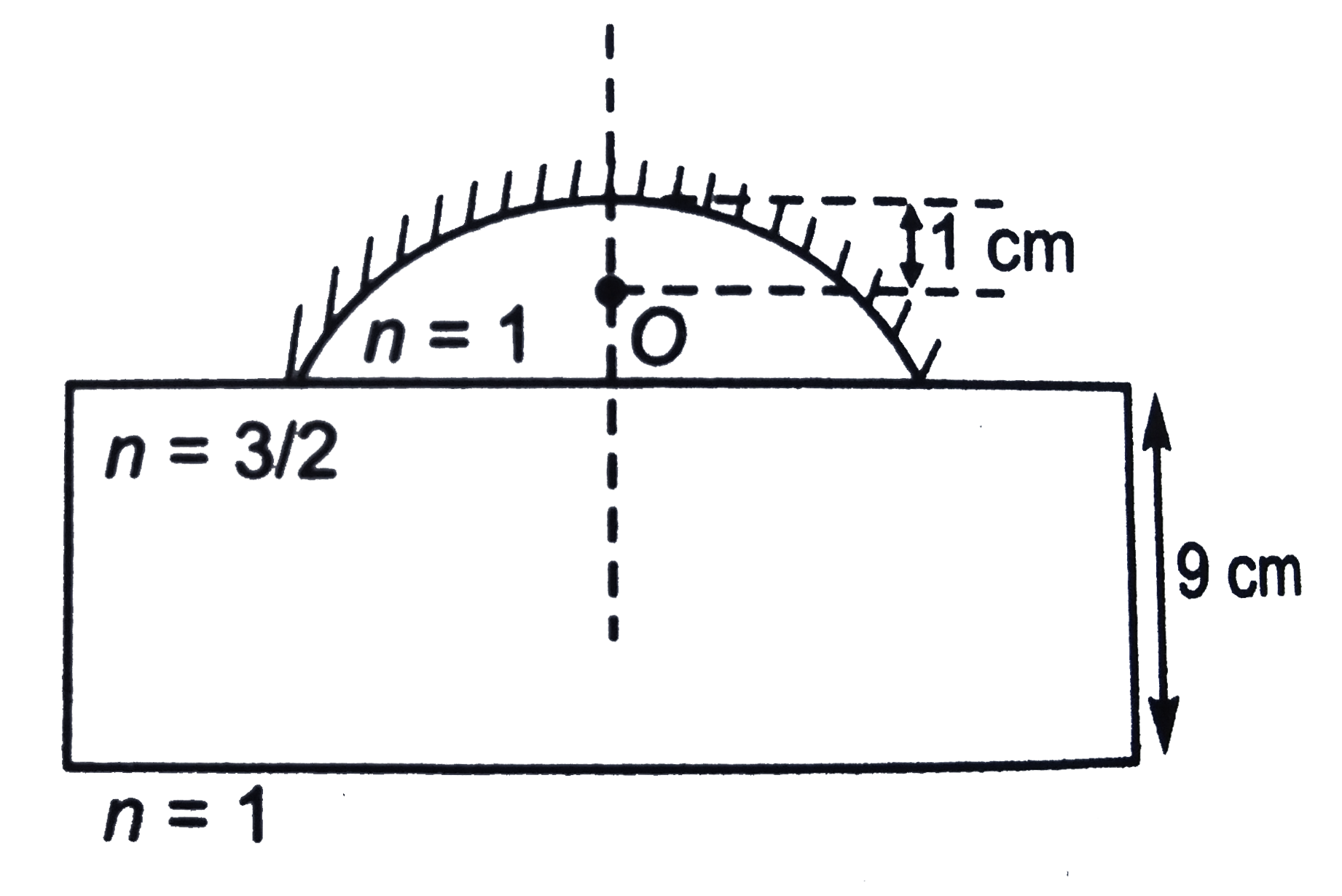
View SolutionA concave mirror of focal length 2cm is placed on a glass slab as shown in the figure. The image of point object O formed due to reflection at mirror and then refraction by the slab
View SolutionA biconvex lens of focal length 40 cm is placed in front of an object at a distance of 20 cm . Now a slab of refractive index 43 is placed somewhere in between the lens and the object. The shift in the image formed after the introduction of slab equals (thickness of the slab is 2 mm)
View SolutionWhen a dielectric slab of thickness 6 cm is introduced between the plates of parallel plate condenser, it is found that the distance between the plates has to be increased by 4 cm to restore to capacity original value. The dielectric constant of the slab is
View Solution