With reference to the figure shown, if the coefficient of friction at the surfaces is 0.42, then the force required to pull out the 6.0 kg block with an acceleration of will be:
The correct Answer is:D
To solve the problem of finding the force required to pull a 6.0 kg block with an acceleration of 1.50 m/s², we will use Newton's second law of motion and the concept of friction.
1. Identify the Given Values:
- Mass of the block (m) = 6.0 kg
- Acceleration (a) = 1.50 m/s²
- Coefficient of friction (μ) = 0.42
- Mass of the upper block (M) = 2.0 kg (assuming this is the block resting on top of the 6.0 kg block)
- Acceleration due to gravity (g) = 10 m/s² (standard value)
2. Calculate the Normal Force (N):
The normal force acting on the 6.0 kg block is equal to the weight of the block plus the weight of the upper block:
N=(m+M)⋅g=(6.0kg+2.0kg)⋅10m/s2=8.0kg⋅10m/s2=80N
3. Calculate the Force of Friction (F_f):
The force of friction can be calculated using the coefficient of friction and the normal force:
Ff=μ⋅N=0.42⋅80N=33.6N
4. Apply Newton's Second Law:
According to Newton's second law, the net force (F_net) acting on the block is given by:
Fnet=m⋅a
Therefore, the net force required to accelerate the block is:
Fnet=6.0kg⋅1.50m/s2=9.0N
5. Calculate the Total Force Required (F):
The total force required to pull the block must overcome both the force of friction and provide the net force for acceleration:
F=Ff+Fnet=33.6N+9.0N=42.6N
6. Final Calculation:
The total force required to pull the 6.0 kg block with an acceleration of 1.50 m/s² is approximately:
F≈42.6N
Conclusion:
The force required to pull the 6.0 kg block with an acceleration of 1.50 m/s² is approximately 42.6 N.
- Mass of the block (m) = 6.0 kg
- Acceleration (a) = 1.50 m/s²
- Coefficient of friction (μ) = 0.42
- Mass of the upper block (M) = 2.0 kg (assuming this is the block resting on top of the 6.0 kg block)
- Acceleration due to gravity (g) = 10 m/s² (standard value)
The normal force acting on the 6.0 kg block is equal to the weight of the block plus the weight of the upper block:
N=(m+M)⋅g=(6.0kg+2.0kg)⋅10m/s2=8.0kg⋅10m/s2=80N
The force of friction can be calculated using the coefficient of friction and the normal force:
Ff=μ⋅N=0.42⋅80N=33.6N
According to Newton's second law, the net force (F_net) acting on the block is given by:
Fnet=m⋅a
Therefore, the net force required to accelerate the block is:
Fnet=6.0kg⋅1.50m/s2=9.0N
The total force required to pull the block must overcome both the force of friction and provide the net force for acceleration:
F=Ff+Fnet=33.6N+9.0N=42.6N
The total force required to pull the 6.0 kg block with an acceleration of 1.50 m/s² is approximately:
F≈42.6N
The force required to pull the 6.0 kg block with an acceleration of 1.50 m/s² is approximately 42.6 N.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 86
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 87
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 84
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions

With reference to the figure shown, if the fcoefficient of friction at the surfaces is 0.42, then the force required to pull out the 6.0 kg block with an acceleration of 1.50ms2 will be:
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View Solution
Knowledge Check
Two blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
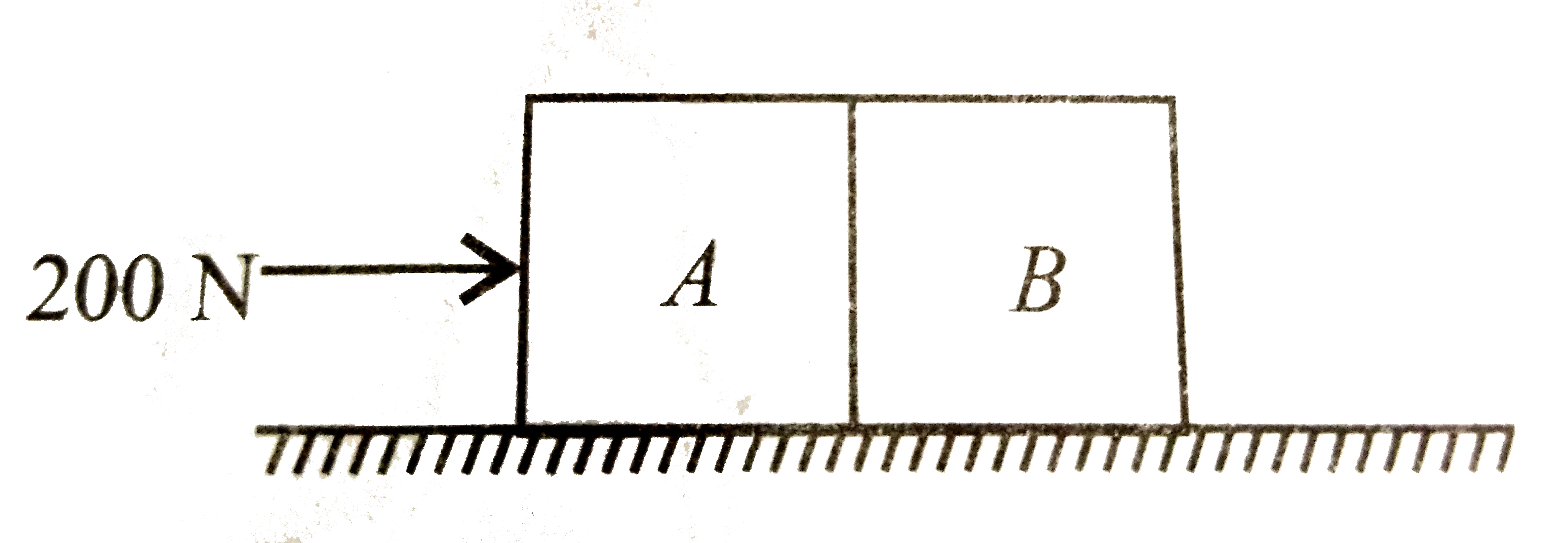 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
Block of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionA block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
View SolutionA block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
View SolutionA block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA block B of mass 5kg is placed on a slab A of mass 20kg which lies on a frictionless surface as shown in the figure. The coefficient of static friction between the block and the slab is 0.4 and that of kinetic friction is 0.2. If a force F = 25N acts on B, the acceleration of the slab will be:

View Solution
As shown in the figure, M is a man of mass 60 kg standing on a block of mass 40 kg kept on ground. The co-efficient of friction between the feet of the man and the block is 0.3 and that between B and the ground is 0.1. If the man accelerates with an acceleration 2ms2 in the forward direction, then,
View Solution
