Question

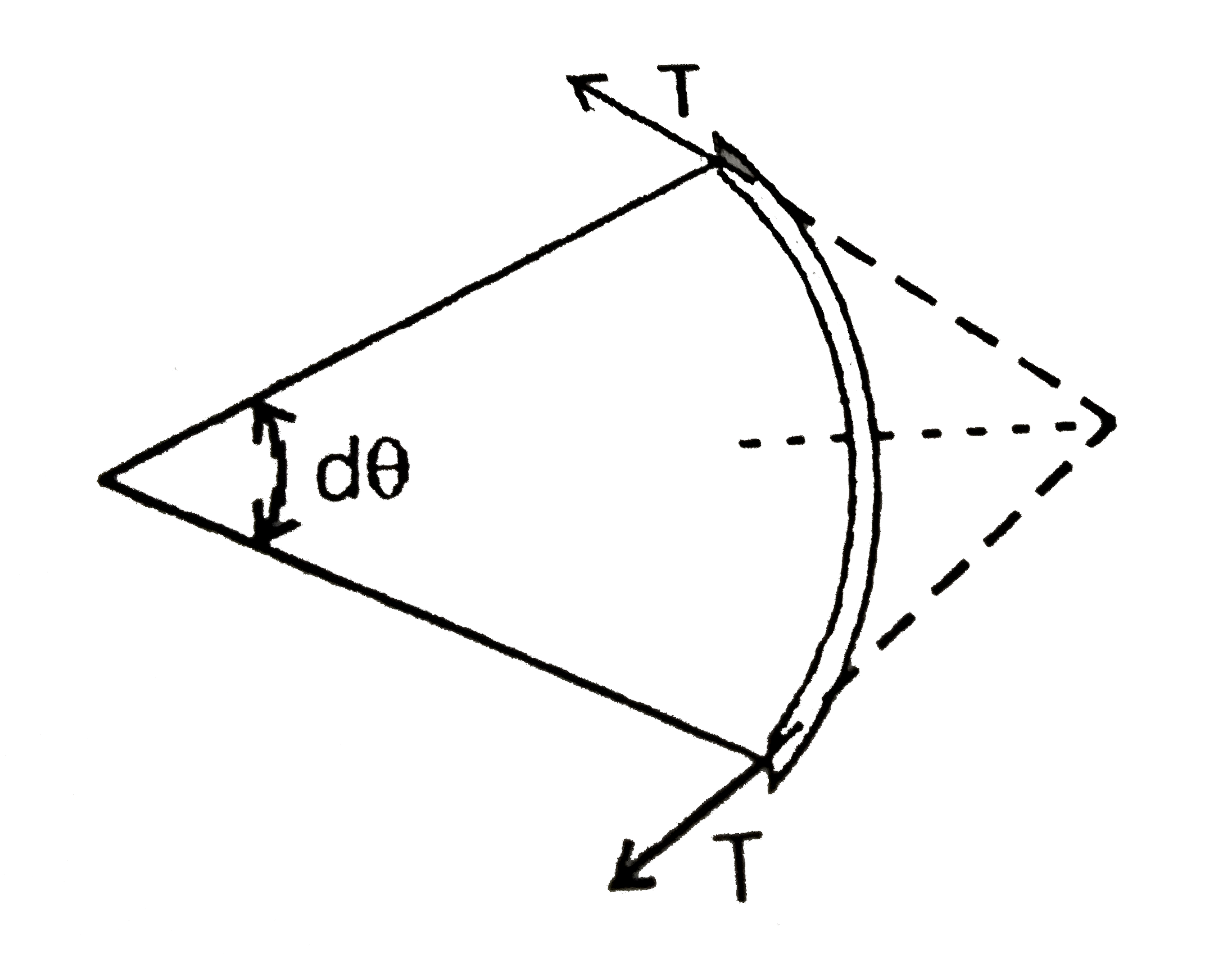
A ring of radius ${\displaystyle R}$ is made of a thin wire of material of density ${\displaystyle \rho }$ having cross section area ${\displaystyle a.}$ The ring rotates with angular velocity ${\displaystyle \omega }$ about an axis passing through its centre and perpendicular to the plane. If we consider a small element of the ring,it rotates in a circle. The required centripetal force is provided by the component of tensions on the element towards the centre. A small element of length ${\displaystyle dl}$ of angular width ${\displaystyle d\theta }$ is shown in the figure.

If ${\displaystyle T}$ is the tension in the ring, then

Options

A. `T=(a rho R^(2)omega^(2))/(2)`
B. `T=a rho R^(2) omega^(2)`
C. `a^(2) rho omega^(2)`
D. `T=2arho R^(2) omega^(2)`

Answer

B

Explanation

As the small element `(dm =a.rho.dl)` in rotating int the circle, centripetal force
`F_(C)=d m omega^(2)R=a rho d l . Omega^(2)R`
`2T=sin (d theta )/(2)=F_(c)=a rho d l omega ^(2)R `
As `d theta` is small `sin (d theta )/(2 )=(d theta )/(2)`
`2T. (d theta)/(2)=a rho ( R d theta ) omega ^(2) R`

`rArr T=a rho R ^(2) omega ^(2) `