For a two − body sstem in absence of external forces, the kinetic energy as measured from ground frame is K0 and from centre of mass frame is Kcm. Pick up the wrong statement.
The kinetic energy as measured from center of mass frame is least
Only the portion of energy Kcm can be transferred from one form to another due to internal changes in the system.
The system always retains at least Ko−Kcm amount of kinetic energy as measured from ground frame irrespective of any kind of internal changes in the system.
The system always retains at least Kcm amount of kinetic energy as measured from ground frame irrespective of any kind of internal changes in the system.
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the kinetic energy measured from the ground frame (K₀) and the kinetic energy measured from the center of mass frame (K_cm) for a two-body system in the absence of external forces. We will also identify the wrong statement among the given options.
1. Understanding Kinetic Energy in Different Frames:
- The kinetic energy of a system can be measured from different reference frames. In this case, we have two frames: the ground frame and the center of mass frame.
2. Kinetic Energy from the Ground Frame (K₀):
- The total kinetic energy measured from the ground frame (K₀) can be expressed as:
K₀=Kcm+12Mv2cm
where:
- Kcm is the kinetic energy measured from the center of mass frame.
- M is the total mass of the system.
- vcm is the velocity of the center of mass with respect to the ground.
3. Kinetic Energy from the Center of Mass Frame (K_cm):
- The kinetic energy in the center of mass frame (K_cm) is the kinetic energy of the system as observed from the center of mass. It does not include the translational kinetic energy due to the motion of the center of mass itself.
4. Analyzing the Statements:
- We need to evaluate the statements provided in the question to identify the incorrect one. The relationship derived above shows that K₀ is always greater than or equal to K_cm, as it includes the additional term 12Mv2cm.
5. Conclusion:
- Since K₀ includes the kinetic energy due to the motion of the center of mass, it cannot be less than K_cm. Therefore, any statement suggesting that K₀ can be less than K_cm or that K_cm can be greater than K₀ would be incorrect.
Final Answer:
The wrong statement is one that suggests K₀<Kcm or any similar relationship that contradicts the derived equation.
- The kinetic energy of a system can be measured from different reference frames. In this case, we have two frames: the ground frame and the center of mass frame.
- The total kinetic energy measured from the ground frame (K₀) can be expressed as:
K₀=Kcm+12Mv2cm
where:
- Kcm is the kinetic energy measured from the center of mass frame.
- M is the total mass of the system.
- vcm is the velocity of the center of mass with respect to the ground.
- The kinetic energy in the center of mass frame (K_cm) is the kinetic energy of the system as observed from the center of mass. It does not include the translational kinetic energy due to the motion of the center of mass itself.
- We need to evaluate the statements provided in the question to identify the incorrect one. The relationship derived above shows that K₀ is always greater than or equal to K_cm, as it includes the additional term 12Mv2cm.
- Since K₀ includes the kinetic energy due to the motion of the center of mass, it cannot be less than K_cm. Therefore, any statement suggesting that K₀ can be less than K_cm or that K_cm can be greater than K₀ would be incorrect.
The wrong statement is one that suggests K₀<Kcm or any similar relationship that contradicts the derived equation.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 558videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 567videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 535videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A body is orbiting very close to the earth surface kinetic energy K.E. The energy required to completely escape from it is
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.View SolutionTwo masses, m1 and m2 , are moving with velocities v1 and v2. Find their total kinetic energy in the reference frame of centre of mass.
View SolutionIn a hypothetical uniform and spherical planet of mass M and radius R, a tunel is dug radiay from its surface to its centre as shown. The minimum energy required to carry a unit mass from its centre to the surface is kmgR. Find value of k. Acceleration due to gravity at the surface of the planet is g.
 View Solution
View SolutionStatement-1: Two particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5m/s. When the relative velocity of approach becomes 3m/s the velocity of the centre of mass is 0.75m/s.
Statement-2: The total kinetic energy as seen from ground is 12μv2rel+12mv2c and in absence of external force, total energy remains conserved.View SolutionA body of mass m moving with a velocity v is approaching a second object of same mass but at rest. The kinetic energy of the two objects as viewed from the centre of mass is
View SolutionAssertion:- In two particle system when viewed from center of mass reference frame, if one particle slops then other one will also stop simultaneously, irrespective of external forces acting on system.
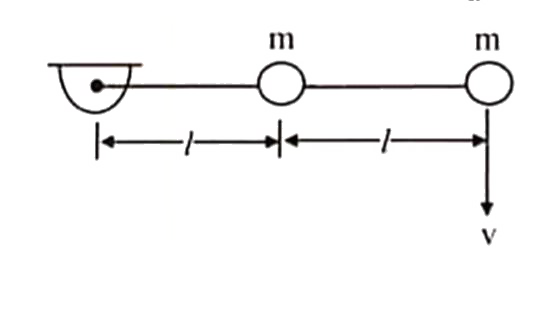
Reason:- Centre of mass of a system is a point about which total momentum of system is always constant and non-zero.View SolutionTwo beads each of mass m are fixed on a light rigid rod of length 2l which is free to rotate in a horizontal plane. The bead on the far end is given some velocity υ as shown in the figure. If Kcm represents the kinetic energy of the centre of mass of the system and KR represents the rotational kinetic energy of the system, then what is the value of KcmKR?
 View Solution
View SolutionA constatnt force of 10 N act on a block as shown in figure intal velocity of the particle is zero. It is observed from three frames of reference S1,S2 and ground. The frame S1 start from rest and move with constnat acceleration 10m/s. The frames S1andS2 and particle start moving simultaneously at t=0.
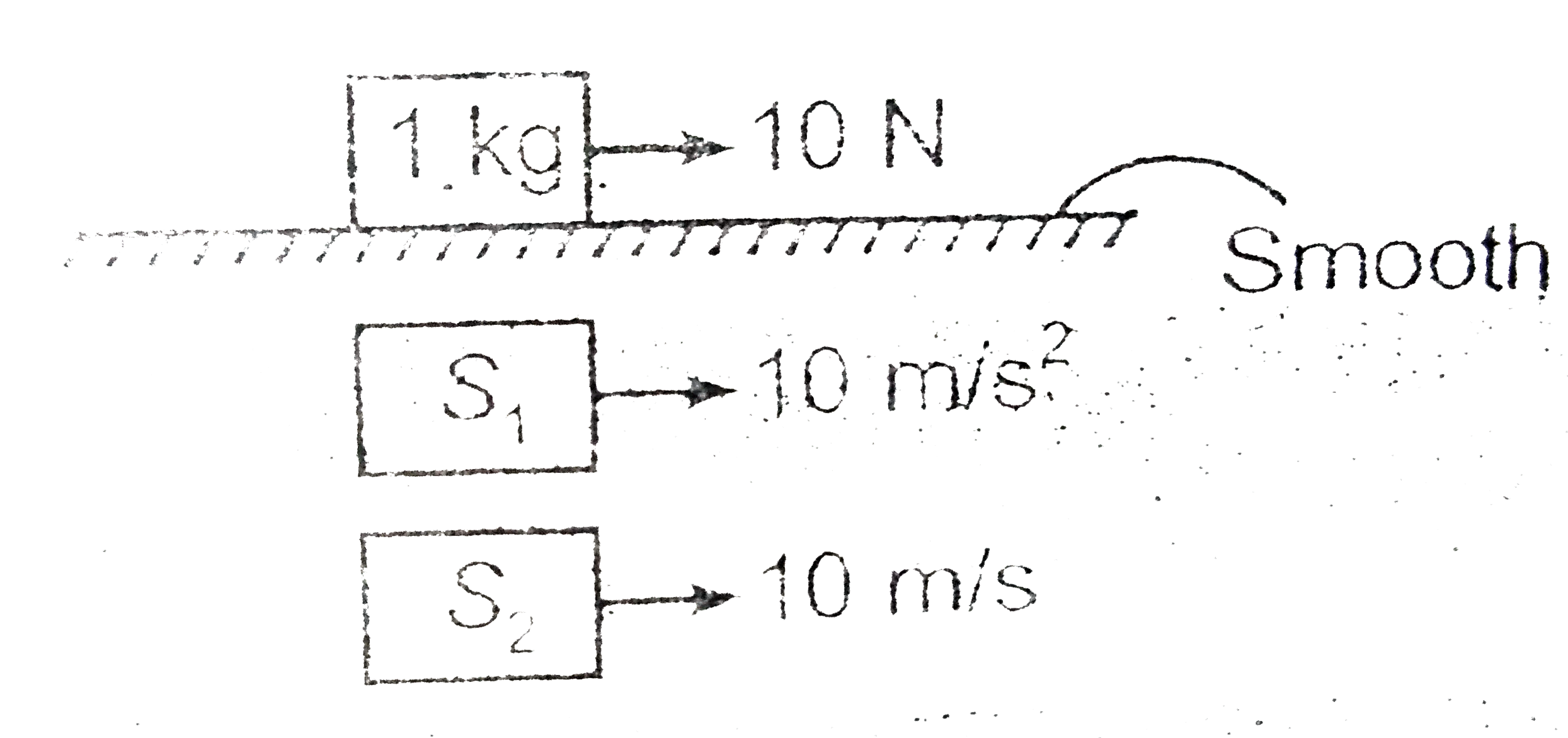
The rate at which work is done by constant force on the particle is always non-negative when observed fomView Solution
