A stone is projected horizontally with speed v from a height h above ground. A horizontal wind is blowing in direction opposite to velocity of projection and gives the stone a constant horizontal acceleration f( in direction opposite to initial velocity ) .As a result the stone falls on ground at a point vertically below the point of projection. Then the value of height h in terms of f,g,v is (g is acceleration due to gravity 0
gv22f2
gv2f2
√2gv2f2
2gv2f2
The correct Answer is:D
Time taken to reach the ground is given by
h=12gt2….(1)
Since horizontal displacement in time t is zero
∴T=2vf…..2
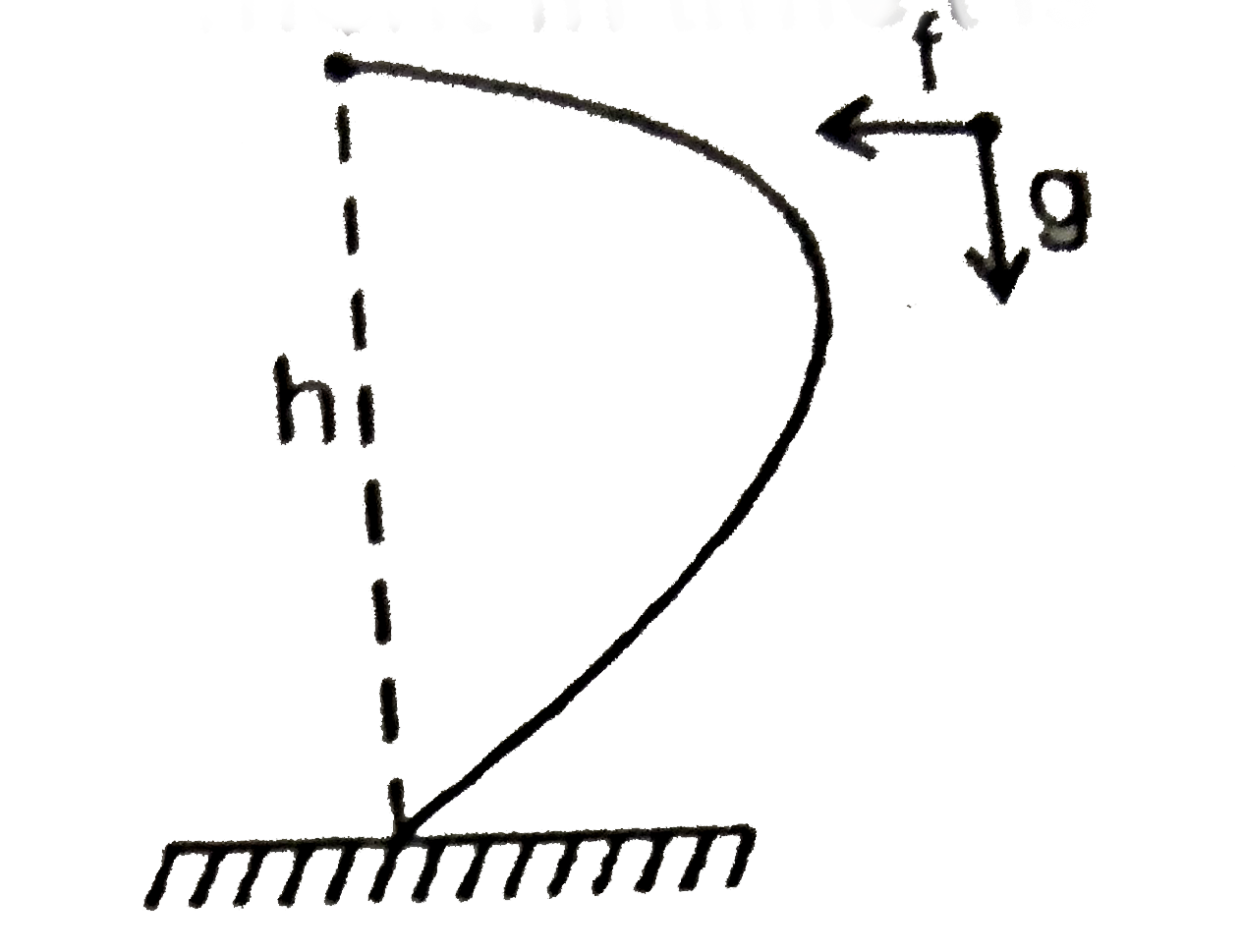
h=2gv2f2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 287videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp295videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 268videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A body is projected horizontally with a speed v0 find the velocity of the body when it covers equal distance in horizontal and vertical directions.
View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA body projected horizontally with a velocityv from a height h has a range R.With what velocity a body is to be projected horizontally from a height h/2 to have the same range ?
View SolutionA stone is projected with speed of 50ms−1 at an angle of 60∘ with the horizontal. The speed of the stone at highest point of trajectory is
View SolutionA stone is projected horizontally with a velocity 9.8ms−1 from a tower of height 100 m. Its velocity one second after projection is (g=9.8ms−2).
View SolutionThe horizontal range of a projectile is R and the maximum height attained by it is H. A strong wind now beings to blow in the direction of horizontal motion of projectile, giving to constant horizontal acceleration equal to g. Under the same conditions of projections , the new range will be (g = acceleration due to gravity)
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :
 View Solution
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
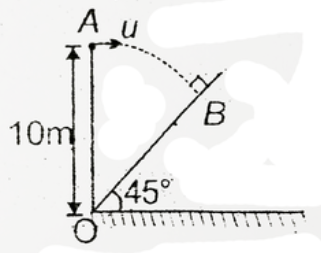
Find horizontal speed with which the particle was projectedView Solution
