A stone is projected with speed of 50ms−1 at an angle of 60∘ with the horizontal. The speed of the stone at highest point of trajectory is
75ms−1
25ms−1
50ms−1
cannot find
The correct Answer is:B
To solve the problem of finding the speed of a stone at the highest point of its trajectory when projected with a speed of 50 m/s at an angle of 60 degrees with the horizontal, we can follow these steps:
1. Identify the Initial Velocity Components:
The initial velocity u can be broken down into horizontal and vertical components using trigonometric functions:
- Horizontal component Vx=ucosθ
- Vertical component Vy=usinθ
Given:
- u=50m/s
- θ=60∘
Calculate:
Vx=50cos(60∘)=50×12=25m/s
Vy=50sin(60∘)=50×√32≈43.3m/s
2. Understand the Motion at the Highest Point:
At the highest point of the trajectory, the vertical component of the velocity Vy becomes zero due to the effect of gravity. However, the horizontal component Vx remains constant throughout the motion because there are no horizontal forces acting on the stone.
3. Determine the Speed at the Highest Point:
At the highest point, the speed of the stone will only be due to the horizontal component:
Vhighest point=Vx=25m/s
4. Conclusion:
Therefore, the speed of the stone at the highest point of its trajectory is 25m/s.
Final Answer:
The speed of the stone at the highest point of trajectory is 25 m/s.
---
The initial velocity u can be broken down into horizontal and vertical components using trigonometric functions:
- Horizontal component Vx=ucosθ
- Vertical component Vy=usinθ
- u=50m/s
- θ=60∘
Vx=50cos(60∘)=50×12=25m/s
Vy=50sin(60∘)=50×√32≈43.3m/s
At the highest point of the trajectory, the vertical component of the velocity Vy becomes zero due to the effect of gravity. However, the horizontal component Vx remains constant throughout the motion because there are no horizontal forces acting on the stone.
At the highest point, the speed of the stone will only be due to the horizontal component:
Vhighest point=Vx=25m/s
Therefore, the speed of the stone at the highest point of its trajectory is 25m/s.
The speed of the stone at the highest point of trajectory is 25 m/s.
Topper's Solved these Questions
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Check Point 4.3
Explore 10 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:A. Taking it together
Explore 1 Video
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Check Point 4.1
Explore 15 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
Similar Questions
The time of fight of an object projected with speed 20ms−1 at an angle 30∘ with the horizontal , is
View SolutionA particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionAn object is projected with a velocity of 30ms−1 at an angle of 60∘ with the horizontal. Determine the horizontal range covered by the object.
View SolutionA boy is running along positive x - axis with 9m/s. While running he manages to throw a stone in a plane perpendicular to his direction of running with velocity 12m/s at an angle 30∘ with vertical. Find the speed of the stone at the highest point of the trajectory.
View SolutionA particle is projected with a speed 10√2ms−1 and at an angle 45∘ with the horizontal. The rate of change of speed with respect to time at t=1s is (g=10ms−2)
View SolutionA boy throws a stone with a speed of V0=10 m/sec at an angle of θ0=30∘ to the horizontal Find the position of the stone wrt the point of projection just after a time t = 1/2 sec.
View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA shell is projected by a cannon at an angle 30∘ with the vertical for a horizontal range R. It explodes at the highest point of its trajectory. Now match the column I and II.
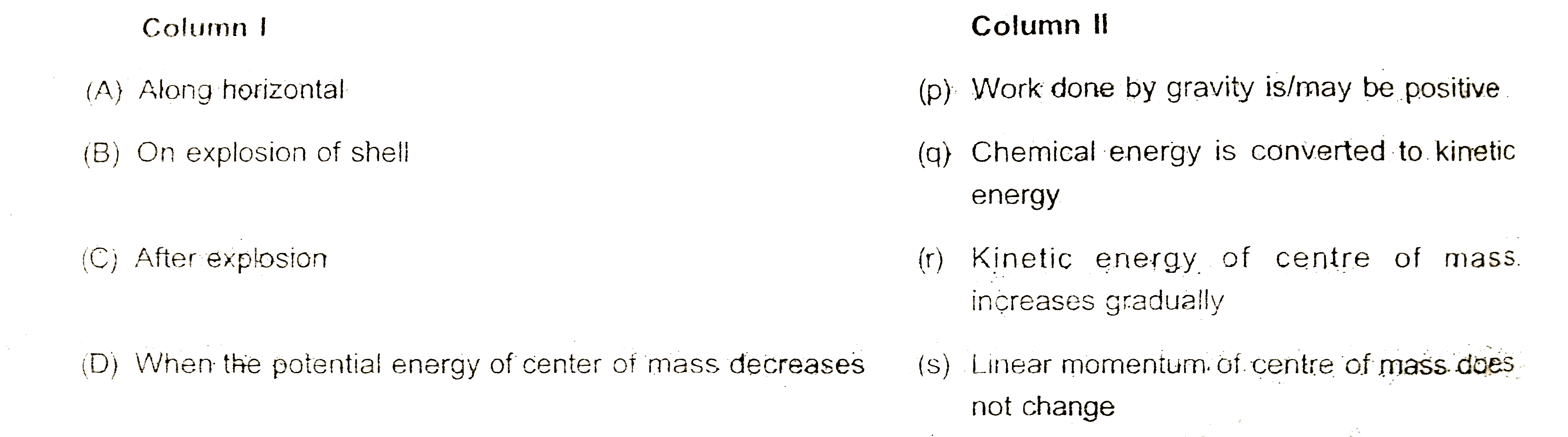
View Solution

