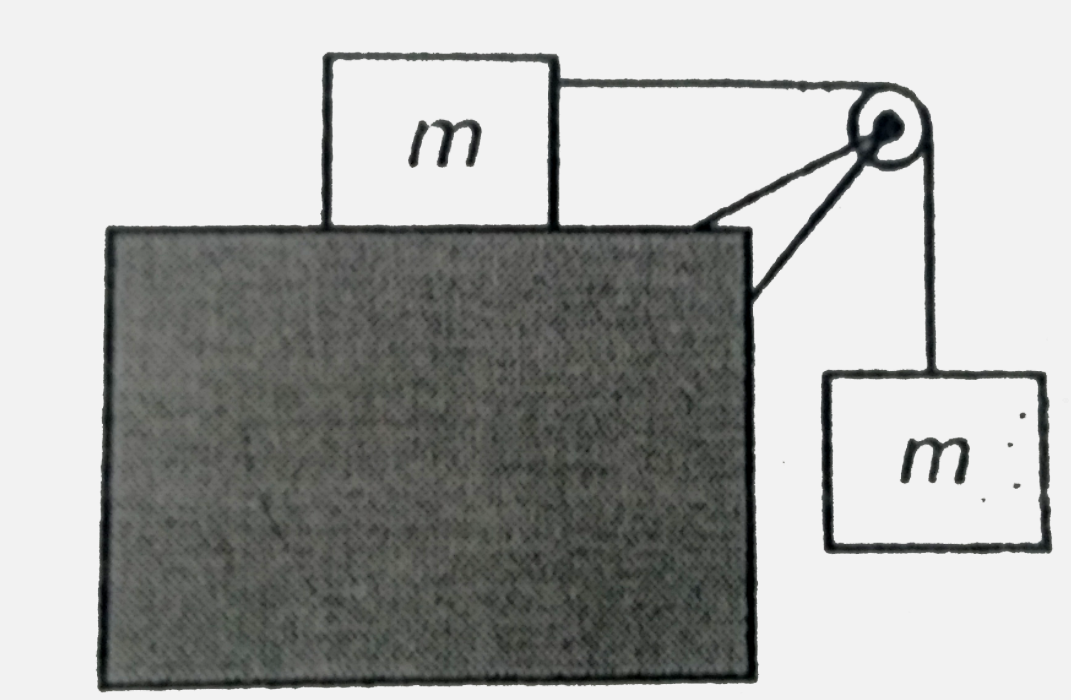
Two cubes of masses m1 and m2 be on two frictionless slopes of block A which rests on a horizontal table. The cubes are connected by a string which passes over a pulley as shown in figure. To what horizontal acceleration f should the whole system (that is blocks and cubes) be subjected so that the cubes do not slide down the planes. What is the tension of the string in this situation?
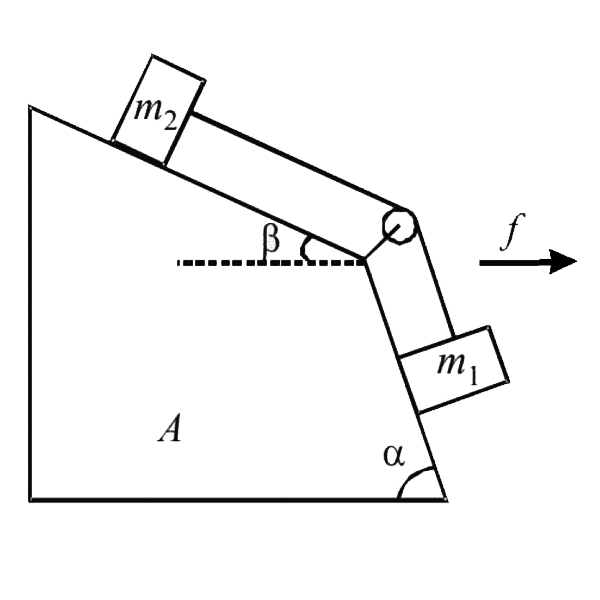
The correct Answer is:T=m1m2gsin(α−β)m1cosα+m2cosβ
If the block has an acceleration towards right,the blocks would have some acceleration towards left. Resoving horizontally and vertically, we have
R2=m2gcosβ+m2fsinβ.....(1)
m2f=Tcosβ+R2sinβ......(2)
and
R1=m1gcosα+m1fsinα.....(3)m1f=R1sinαα−Tcosα......(4)
From equaiton (2) and (1) , we get
m2f=Tcosβ+[m2gcosβ+m2fsinβ]sinβ
=Tcosβ+m2gcosβsinβ+m2fsin2β
∴Tcosβ=m2f−m2fsin2β−m2gcosβsinβ
orTcosβm2cos2β−m2βcosβsinβ
orT=m2fcosβ−m2gsinβ.....(5)
From equations (3) and (4) , we have
m1f=(m1gcosα+m1fsinα)sinα−Tcosα
=m1gcosαsinα+m1fsin2α−Tcosα
∴Tcosα=m1gcosαsinα+m1f(sin2α−1)
orT=m1gsinα−m1fcosα....(6)
Equating (5) and (6), we get
m2fcosα−m2gsinβ=m1gsinα−m1fcosα
∴f=gg[(m1sinα+m2sinβ)(m2cosβ+m1cosα)]....(7)
Substituting the value of f in eqn.(6), we get
T=m1gsinα−m1g
{(m1sinα+m2sinβ)(m2cosβ+m1cosα)}cosα
Simplifying , we get
T=m1m2gsin(α−β)m1cosα+m2cosβAns.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 26
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 27
Explore 3 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:TRUE/FALSE
Explore 2 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
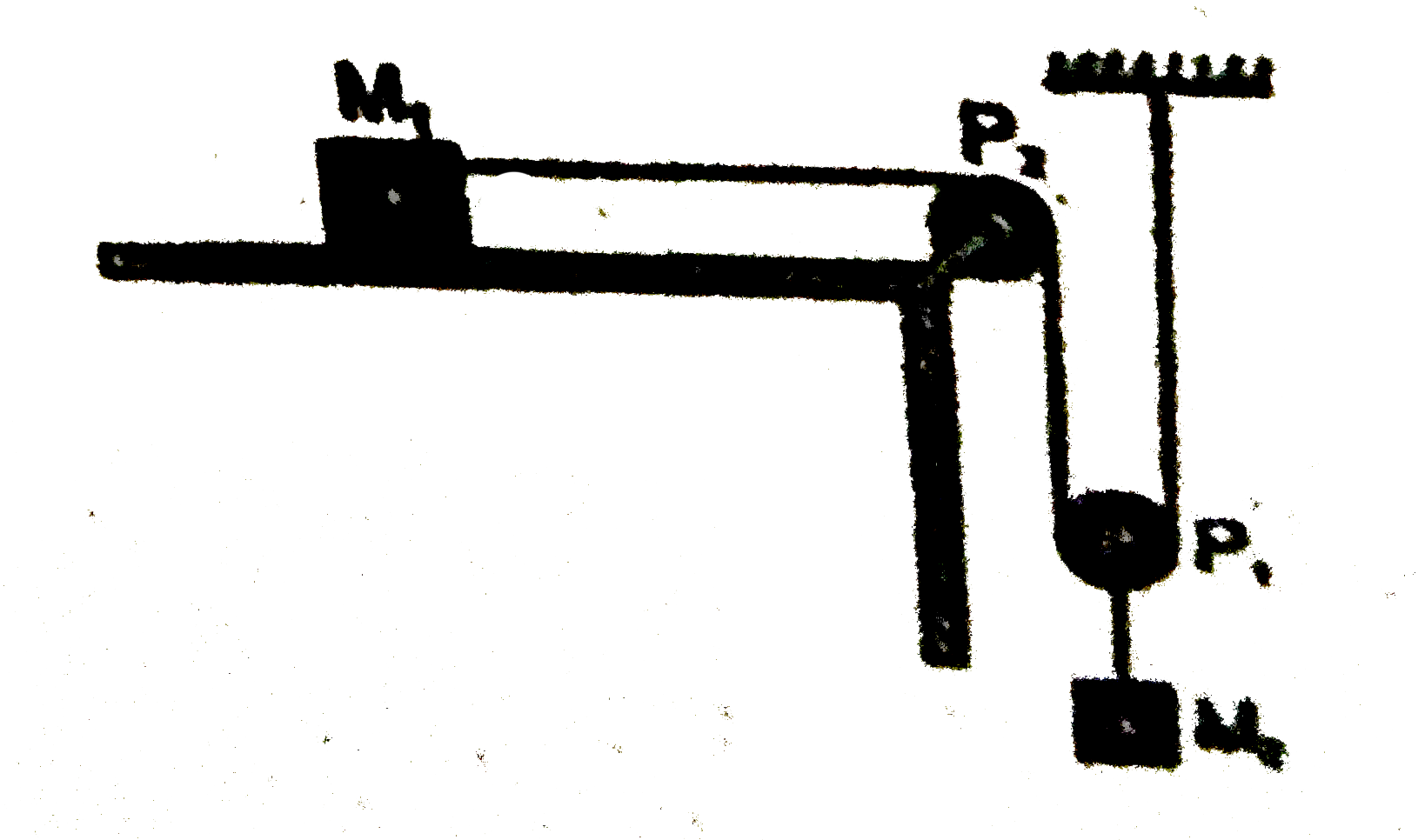
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
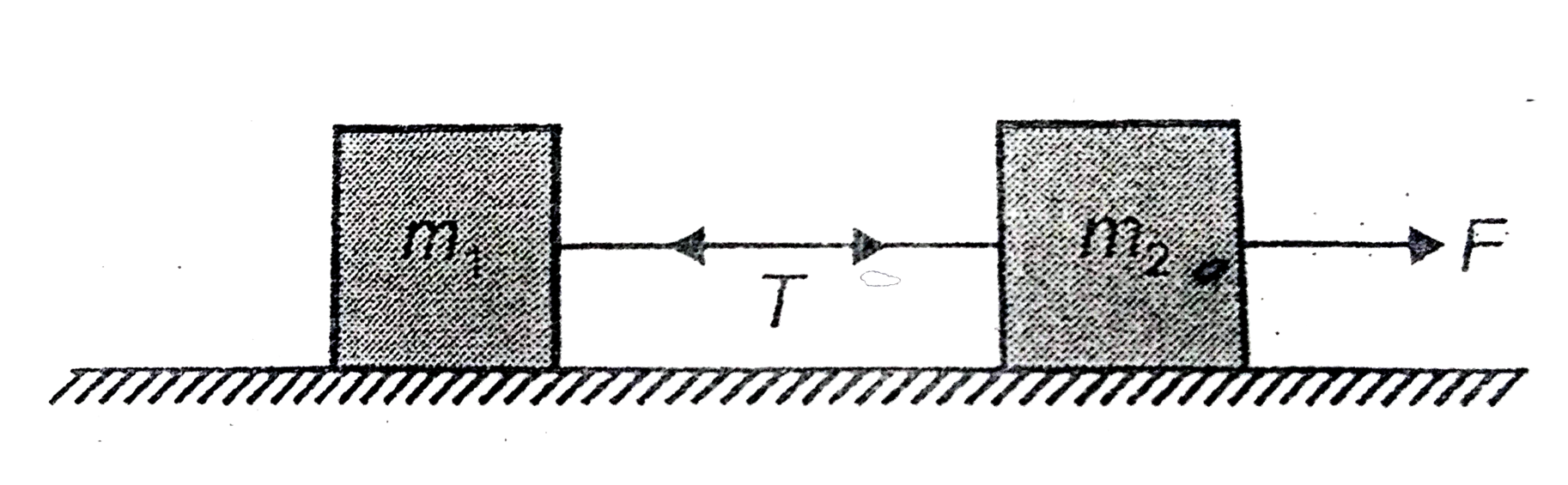
View SolutionTwo block of masses m1andm2 are lying on a frictionless horizontal table connected by a light string m2 is pulled by horizontal force F. Calculate the tension in the string .
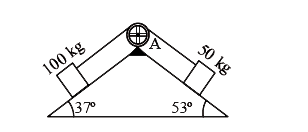
View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

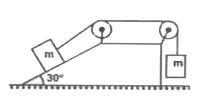
View SolutionTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
View SolutionTwo blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
View SolutionA 2kg block lying on smooth table which is connected by a body of mass 1 kg by a string which passes through a pulley. Take 1 kg mass hanging vertically. Find the acceleration of block & tension in string.
View Solution