Question

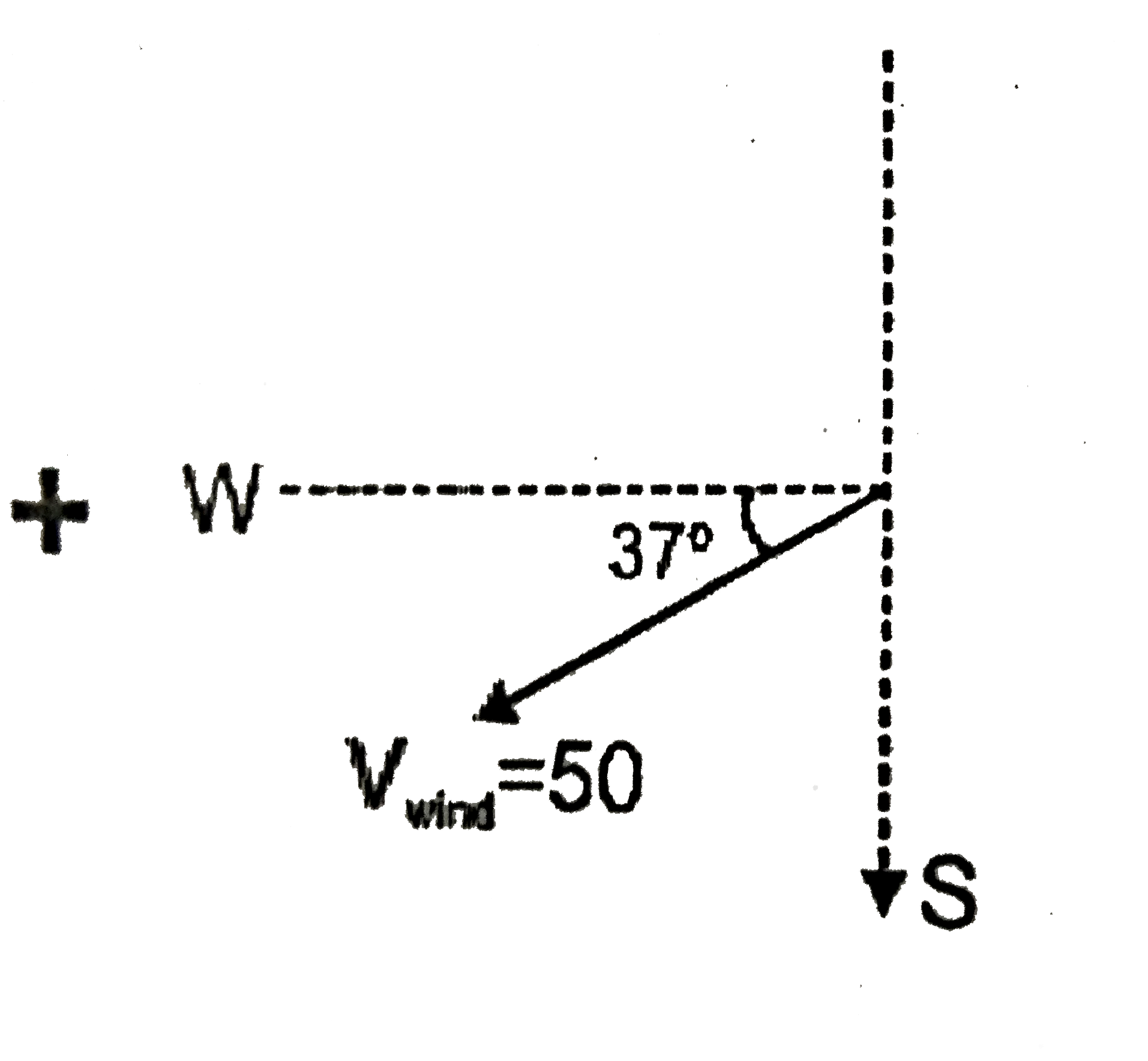
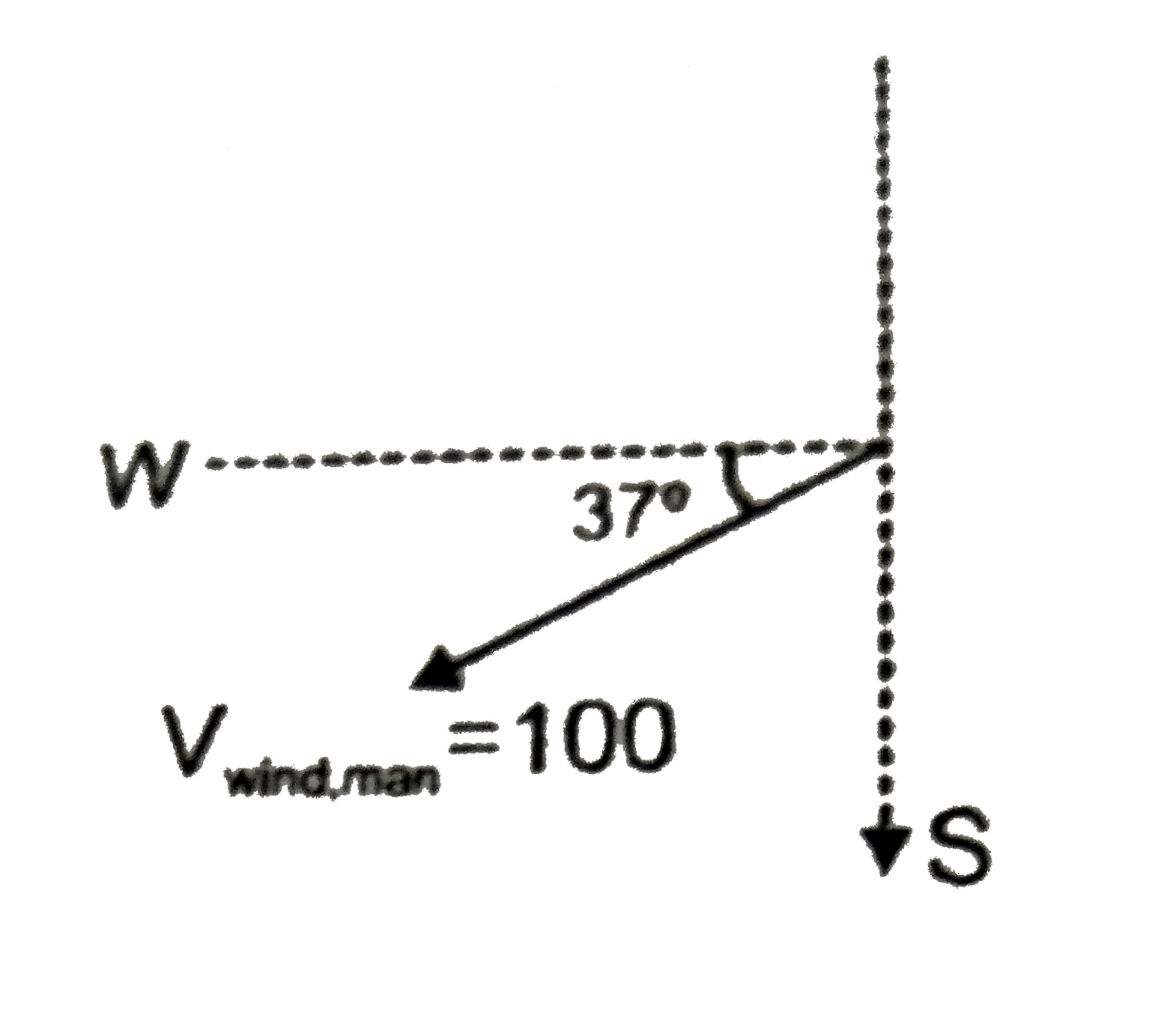
A man is on ship which is moving in east direction with speed $60km/hr.$ Waves of ocean is taking ship towards west with speed $20km/hr$. Man start running on ship with flag in his hand in north direction with speed $30km/hr$ and wind is blowing with $50km/hr,{37}^{\circ }$ towards south of west then find the direction of flutter the flag as seen by man on ground.

Options

A. `37^(@)` south to west
B. `53^(@)` south of west
C. `37^(@)` west of north
D. flag will not flutter

Answer

A

Explanation

To solve the problem step by step, we will analyze the motion of the ship, the man, and the wind, and then determine the direction of the flutter of the flag as seen by the man on the ground.

Step 1: Determine the net velocity of the ship
The ship is moving east at a speed of 60 km/hr, while the waves are moving it west at a speed of 20 km/hr.

Calculation:
- Net velocity of the ship = Velocity of ship (east) - Velocity of waves (west)
- Net velocity of the ship = 60 km/hr (east) - 20 km/hr (west) = 40 km/hr (east)

Step 2: Analyze the man's running speed
The man is running north with a speed of 30 km/hr. However, since the ship is moving east and the waves are moving it west, we need to consider the overall effect on the flutter of the flag.

Step 3: Analyze the wind's effect
The wind is blowing at a speed of 50 km/hr at an angle of 37 degrees south of west. We need to resolve this wind speed into its westward and southward components.

Calculation:
- Westward component of wind = 50 km/hr * cos(37°) = 50 * (4/5) = 40 km/hr
- Southward component of wind = 50 km/hr * sin(37°) = 50 * (3/5) = 30 km/hr

Step 4: Combine the velocities affecting the flutter of the flag
Now we will combine the westward and southward velocities to determine the resultant velocity affecting the flutter of the flag.

Westward velocities:
- From the ship's net velocity: 40 km/hr (east, which we consider as -40 km/hr for west)
- From the wind: 40 km/hr (west)

Total westward velocity = 40 km/hr (from wind) + 40 km/hr (from ship) = 80 km/hr (west)

Southward velocities:
- From the man running: 30 km/hr (north, which we consider as -30 km/hr for south)
- From the wind: 30 km/hr (south)

Total southward velocity = 30 km/hr (from wind) + 30 km/hr (from man) = 60 km/hr (south)

Step 5: Determine the direction of the flutter of the flag
Now, we have the resultant velocities:
- Westward: 80 km/hr
- Southward: 60 km/hr

To find the angle θ of the flutter direction, we can use the tangent function:

Calculation:
- tan(θ) = Opposite / Adjacent = Southward velocity / Westward velocity
- tan(θ) = 60 km/hr / 80 km/hr = 3/4

Now, we find θ:
- θ = tan^(-1)(3/4)

Using a calculator:
- θ ≈ 37 degrees

Conclusion:
The direction of the flutter of the flag as seen by the man on the ground is approximately 37 degrees south of west.