The velocity of a particle moving along straight line is given in terms of time as where is in seconds and is in .
The speed is minimum after second at instant of time
None of these
The correct Answer is:B
To find the time at which the speed of the particle is minimum, we start with the given velocity function:
v(t)=3(t2−t)
Step 1: Find the first derivative of the velocity function
To find the critical points where the speed could be minimum, we first differentiate the velocity function with respect to time t.
dvdt=ddt(3(t2−t))
Using the power rule for differentiation:
dvdt=3(2t−1)=6t−3
Step 2: Set the first derivative equal to zero
To find the critical points, we set the first derivative equal to zero:
6t−3=0
Solving for t:
6t=3
t=36=0.5 seconds
Step 3: Find the second derivative of the velocity function
Next, we find the second derivative to determine whether this critical point is a minimum or maximum.
d2vdt2=ddt(6t−3)
Differentiating again:
d2vdt2=6
Step 4: Analyze the second derivative
Since the second derivative d2vdt2=6 is positive, this indicates that the critical point at t=0.5 seconds is indeed a minimum point for the velocity.
Step 5: Determine the speed at the critical point
Now, we need to check the speed at t=0.5 seconds to ensure it is indeed the minimum speed after t=0.
Substituting t=0.5 into the velocity function:
v(0.5)=3((0.5)2−0.5)
=3(0.25−0.5)
=3(−0.25)
=−0.75 m/s
Since speed is the absolute value of velocity, we take:
Speed=|v(0.5)|=0.75 m/s
Step 6: Check for other critical points
Next, we should check if there are any other points where the velocity could be zero, as speed cannot be negative. Setting the velocity function to zero:
3(t2−t)=0
3t(t−1)=0
This gives us:
t=0 or t=1 second
Step 7: Analyze the speed at these points
1. At t=0:
v(0)=3(02−0)=0 m/s
Speed = 0 m/s
2. At t=1:
v(1)=3(12−1)=0 m/s
Speed = 0 m/s
Conclusion
The minimum speed occurs at t=1 second, where the speed is 0 m/s.
Thus, the time at which the speed is minimum after t=0 seconds is:
Final Answer: t=1 second
To find the critical points where the speed could be minimum, we first differentiate the velocity function with respect to time t.
To find the critical points, we set the first derivative equal to zero:
t=36=0.5 seconds
Next, we find the second derivative to determine whether this critical point is a minimum or maximum.
Since the second derivative d2vdt2=6 is positive, this indicates that the critical point at t=0.5 seconds is indeed a minimum point for the velocity.
Now, we need to check the speed at t=0.5 seconds to ensure it is indeed the minimum speed after t=0.
=3(0.25−0.5)
=3(−0.25)
=−0.75 m/s
Next, we should check if there are any other points where the velocity could be zero, as speed cannot be negative. Setting the velocity function to zero:
3t(t−1)=0
1. At t=0:
v(0)=3(02−0)=0 m/s
Speed = 0 m/s
v(1)=3(12−1)=0 m/s
Speed = 0 m/s
The minimum speed occurs at t=1 second, where the speed is 0 m/s.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 70
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 71
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 69
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
The velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionThe speed of a particle moving in a circle of radius r=2m varies with time t as v=t2, where t is in second and v in m/s. Find the radial, tangential and net acceleration at t=2s.
View SolutionA particle moves in a circle of radius 20 cm. Its linear speed is given by v=(3t2+5t) where t is in second and v is in m/s. Find the resultant acceleration at t = 1s.
View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
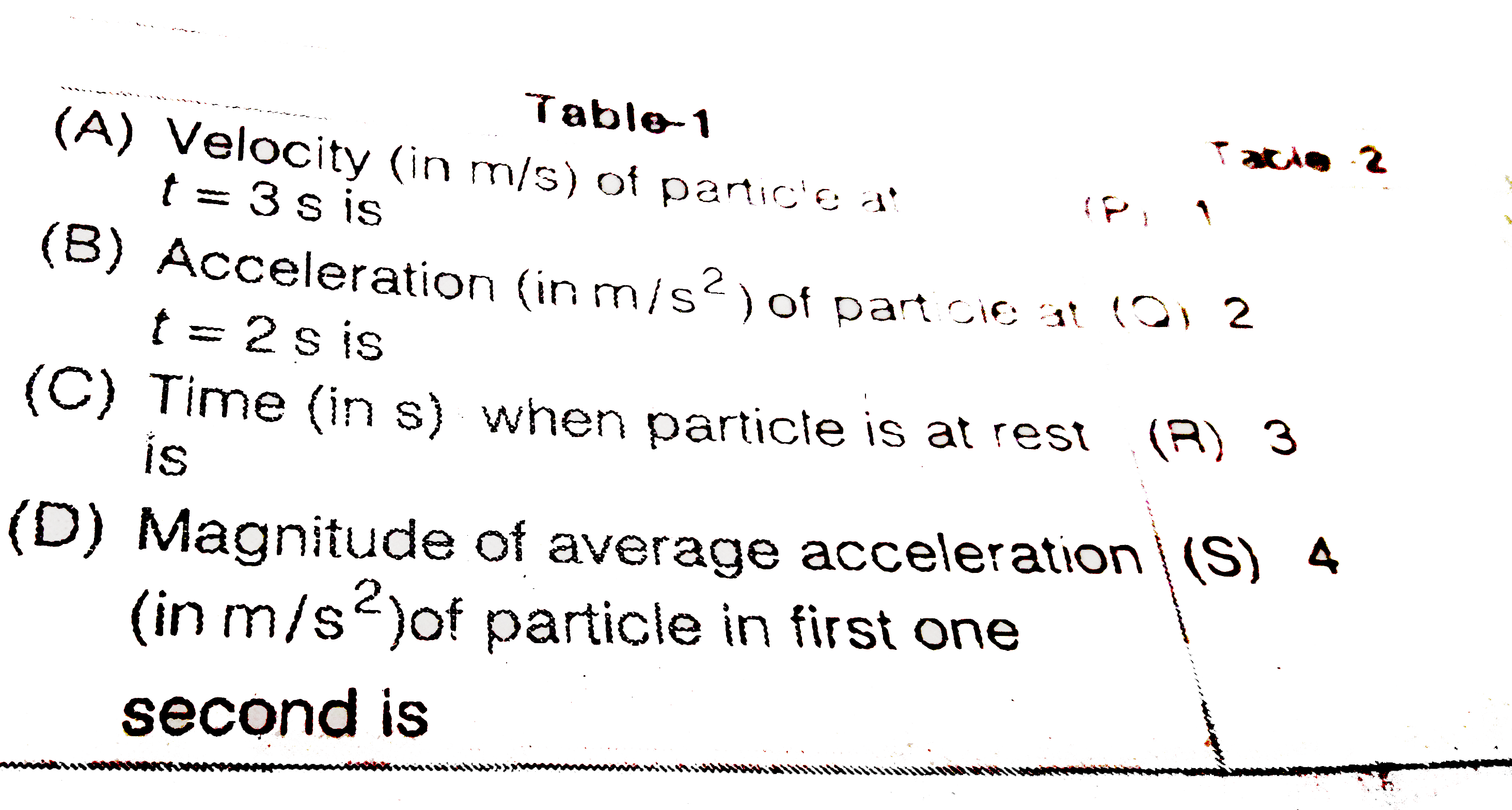
View SolutionThe velocity of an object moving rectilinearly is given as a function of time by v=4t−3t2 where v is in m/s and t is in seconds. The average velocity if particle between t=0 to t=2 seconds is
View Solution

