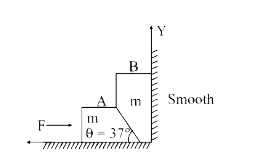
Two smooth block are placed at a smooth corner as shown in fig. Both t

Two smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases $F (θ = 37^{\circ}$ with horizontal).
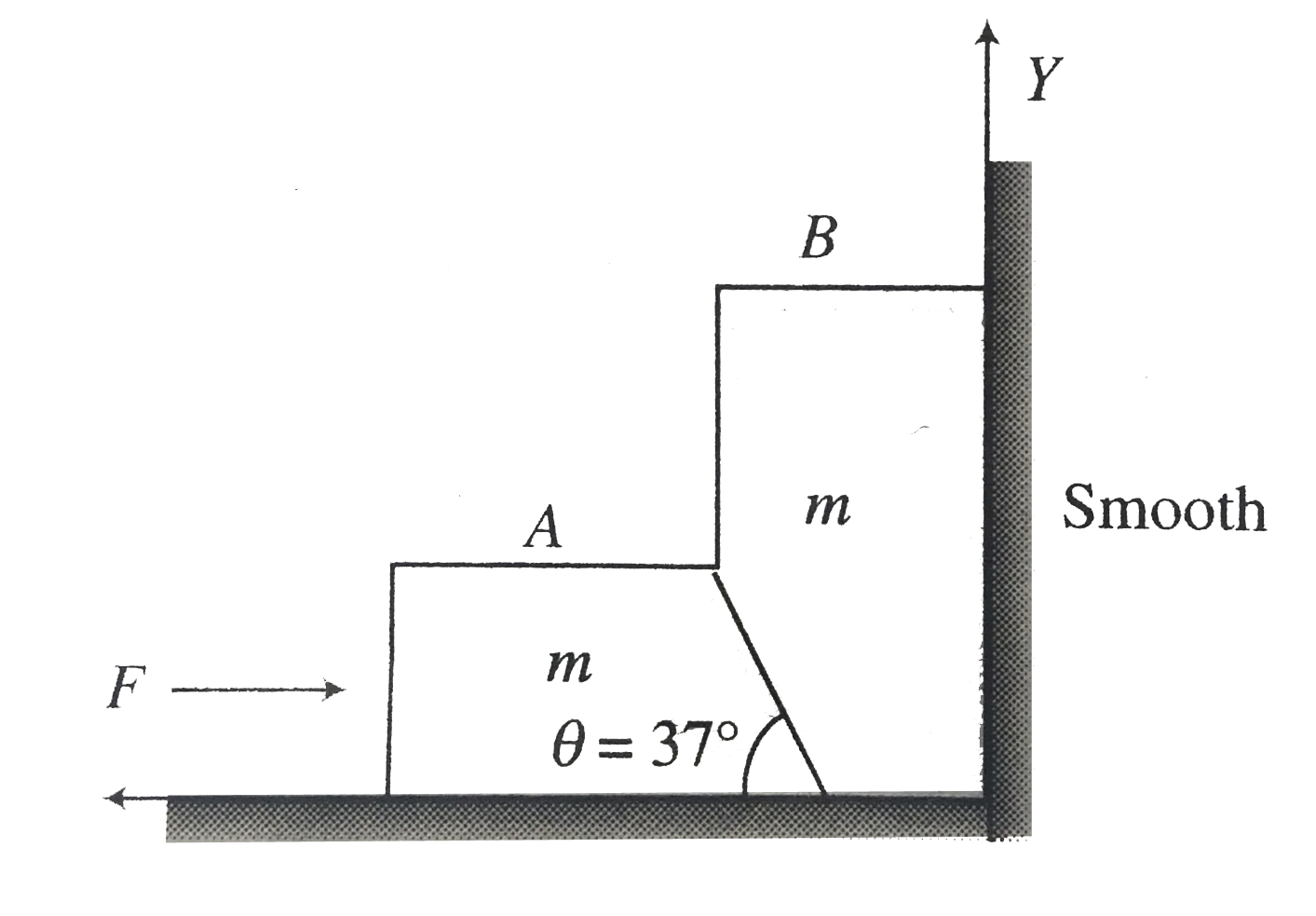
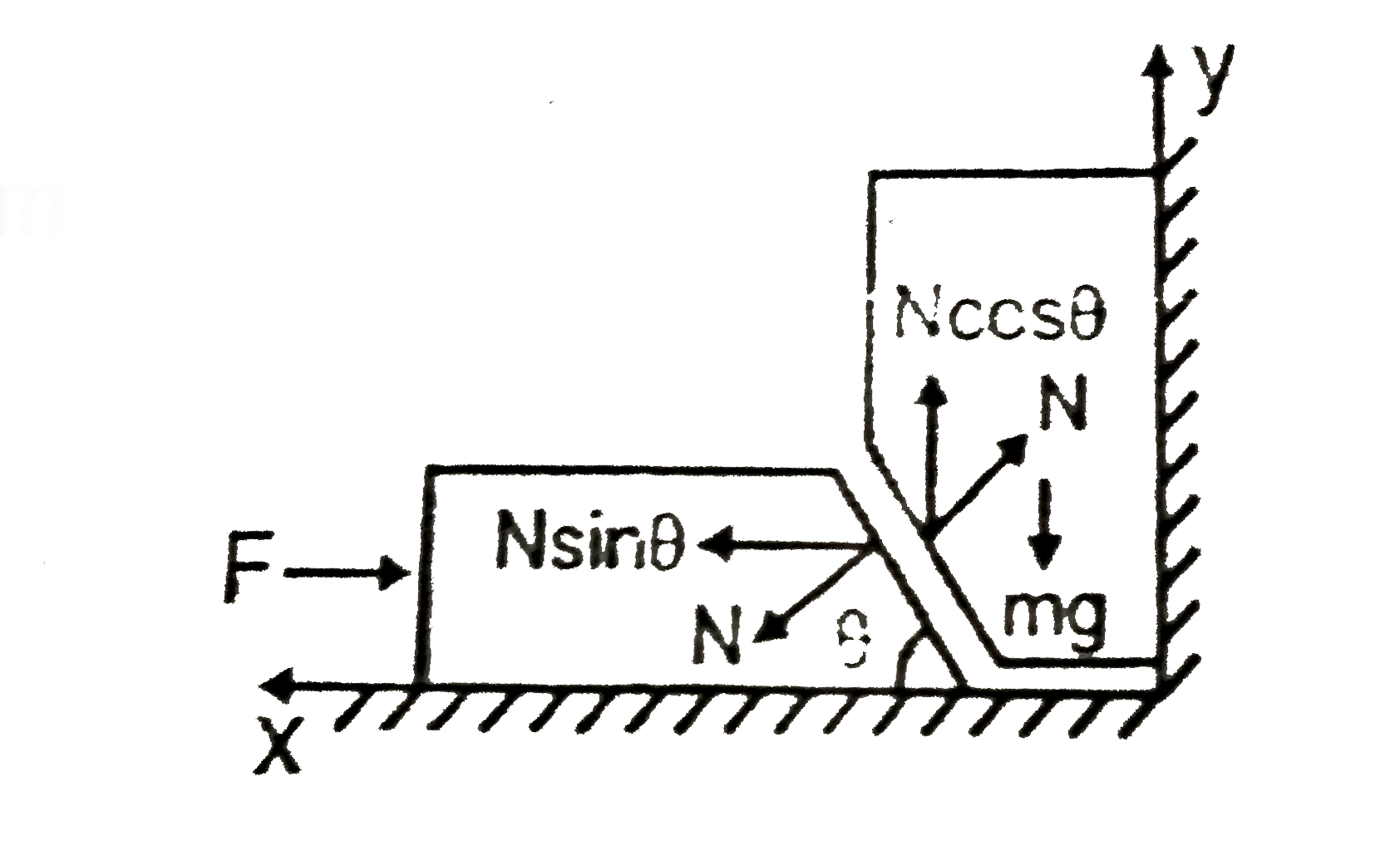
ocr_image
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If both the blocks are stationary, the force exerted by ground of block A is

View Solution

Two smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases $F (θ = 37^{\circ}$ with horizontal).
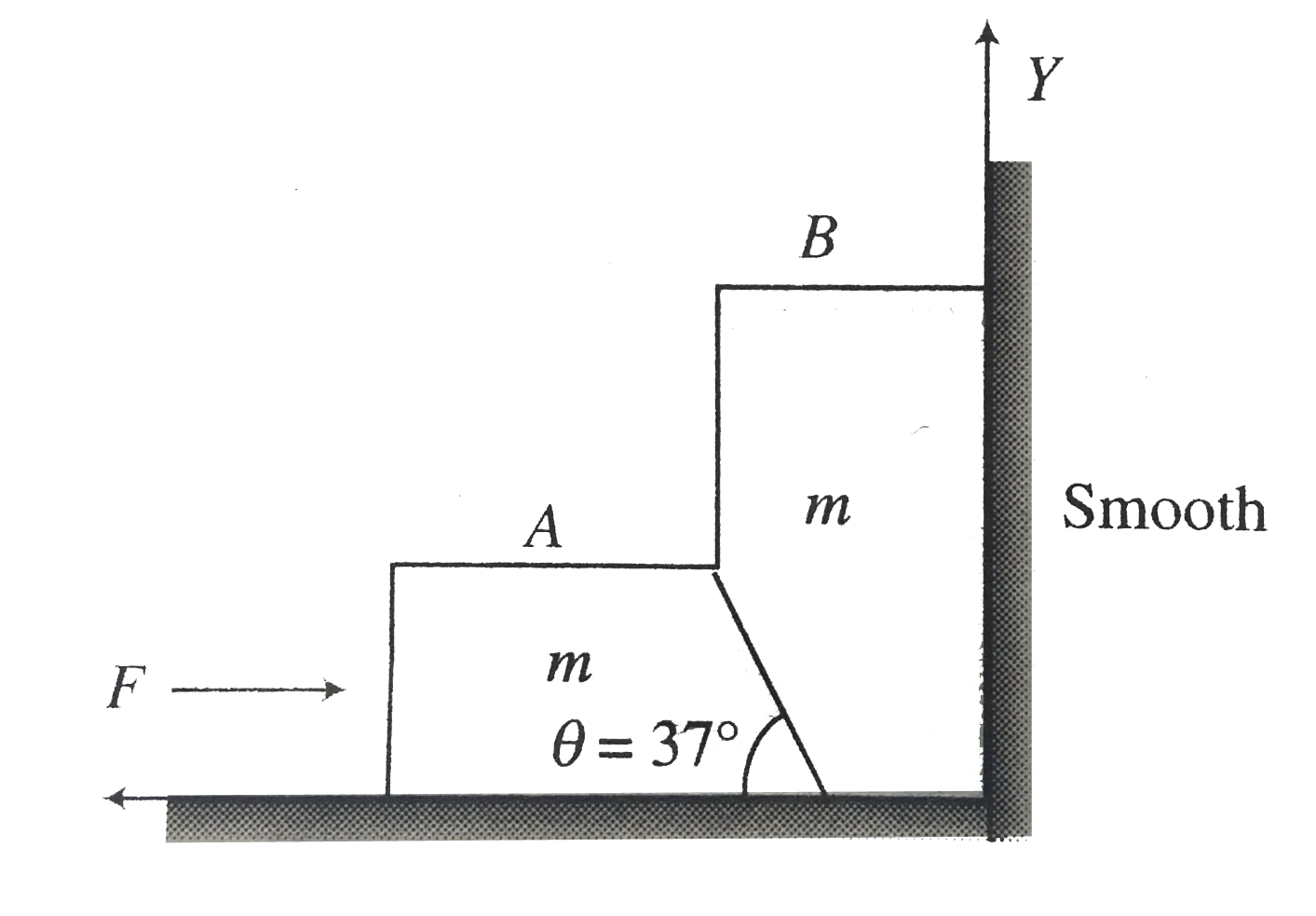
ocr_image
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If both the blocks are stationary, the force exerted by ground of block A is

View Solution

Two smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases $F (θ = 37^{\circ}$ with horizontal).
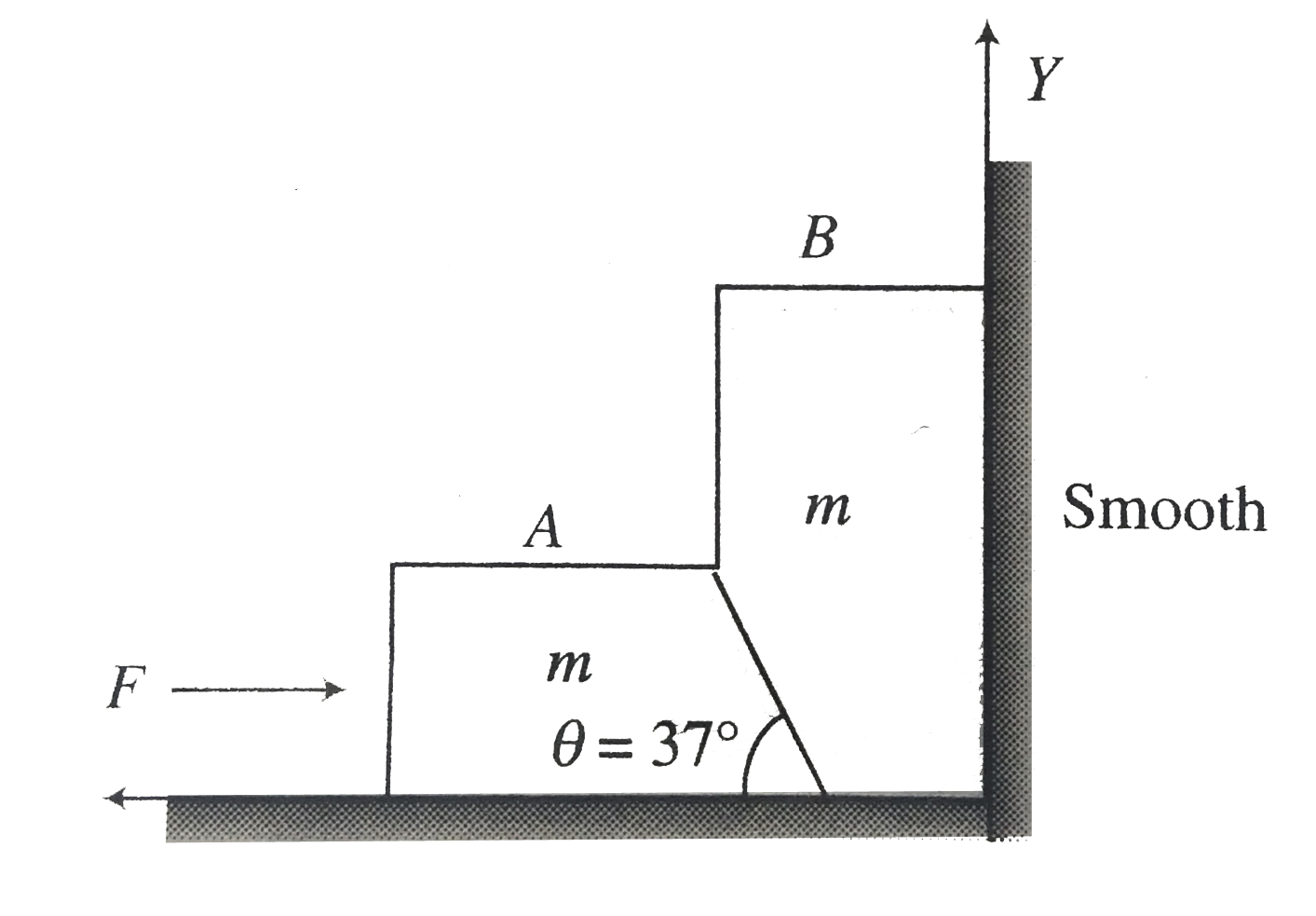
ocr_image
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If both the blocks are stationary, the force exerted by ground of block A is

View Solution

Two smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases $F (θ = 37^{\circ}$ with horizontal).
ocr_image
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If the acceleration of block A is a rightwards, then the acceleration of block B will be

View Solution

Two smooth block are placed at a smooth corner as shown in fig. Both the bloks are having mass m. We apply a force F on the block m. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase, and pressing force on the horizontal wall decreases, as we increases $F (θ = 37^{\circ}$ with horizontal).
ocr_image
As soon as the pressing force on the horizontal wall by block B become zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simulaneously block A will towards right.
If the acceleration of block A is a rightwards, then the acceleration of block B will be

View Solution

Two smooth blocks are placed at a smooth corner as shown in figure. Both the blocks are having mass m. We apply a force F on the block A. Block A presses block B in the normal direction, due to which pressing force on vertical wall will increase and pressing force on the horizontal wall decreases, as we increase $F (θ = 37^{\circ}$ with horizontal).
A soon as the pressing force on the horizontal wall by block B becomes zero, it will lose contact with ground. If the value of F further increases, block B will accelerate in the upward direction and simultaneously block A will move towards right
ocr_image
If the acceleration of block A is a rightwards, then the acceleration of block B will

View Solution

A block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?
ocr_image

View Solution

Two block of masses $m_{1} and m_{2}$ are placed side by side on a smooth horizontal surface as shown in fig. A horizontal force F is applied on the block .
ocr_image
(a) Find the acceleration of each block.
(b) Find the normal reaction between the two blocks.

View Solution

Two blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.
ocr_image
.

View Solution

A block of mass m is placed on a smooth inclined plane of inclination $θ$ with the horizontal. The force exerted by the plane on the block has a magnitude

View Solution

The correct Answer is:C

For $e q \underset{̲}{i} .$ of block $(A)$
$F = N \sin θ$
$N = F / \sin θ$
To lift block $B$ from ground
$N \cos θ \geq m g$
$\frac{F}{\sin θ} \cos θ \geq m g$
$F \geq m g \tan θ = m g (\frac{3}{4})$
So, $F_{m i n} = \frac{3}{4} m g$

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-comprehension

The correct Answer is:C

For e q i ̲ . of block ( A ) F = N sin θ N = F / sin θ To lift block B from ground N cos θ ≥ m g F sin θ cos θ ≥ m g F ≥ m g tan θ = m g ( 3 4 ) So, F m i n = 3 4 m g

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-comprehension

For $e q \underset{̲}{i} .$ of block $(A)$
$F = N \sin θ$
$N = F / \sin θ$
To lift block $B$ from ground
$N \cos θ \geq m g$
$\frac{F}{\sin θ} \cos θ \geq m g$
$F \geq m g \tan θ = m g (\frac{3}{4})$
So, $F_{m i n} = \frac{3}{4} m g$