An isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is

l=√(l12)2+(l2)2
l2=(l12)2+(l2)2
0=2l1212dl1dT+2l2×dl2dT
l1×l1α12×ΔT=2l2×l2α2ΔT
⇒l21l22=4α2α1⇒l1l2=2√α2α1.
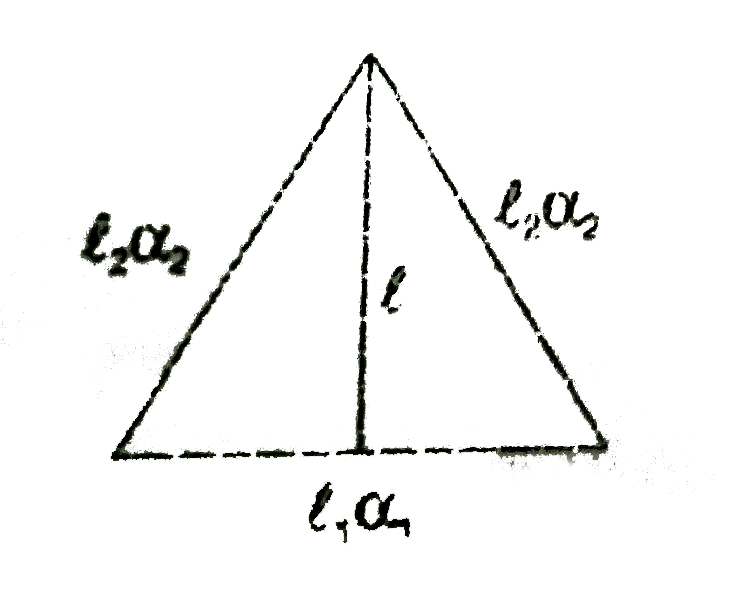
Topper's Solved these Questions
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Board Level Exercise
19 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-1
1 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Solved miscellaneous problems
1 Videos
- CALORIMETRYBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise
19 Videos
- CAPACITORBOOK - RESONANCE ENGLISHCHAPTER - CAPACITOREXERCISE - Exercise
45 Videos
Similar Questions
There are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionTwo metallic rods of length l and 3l have coefficient of linear expansion α and 3α respectively. The coefficient of linear expansion ofr their series combinations, is
View SolutionA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View Solution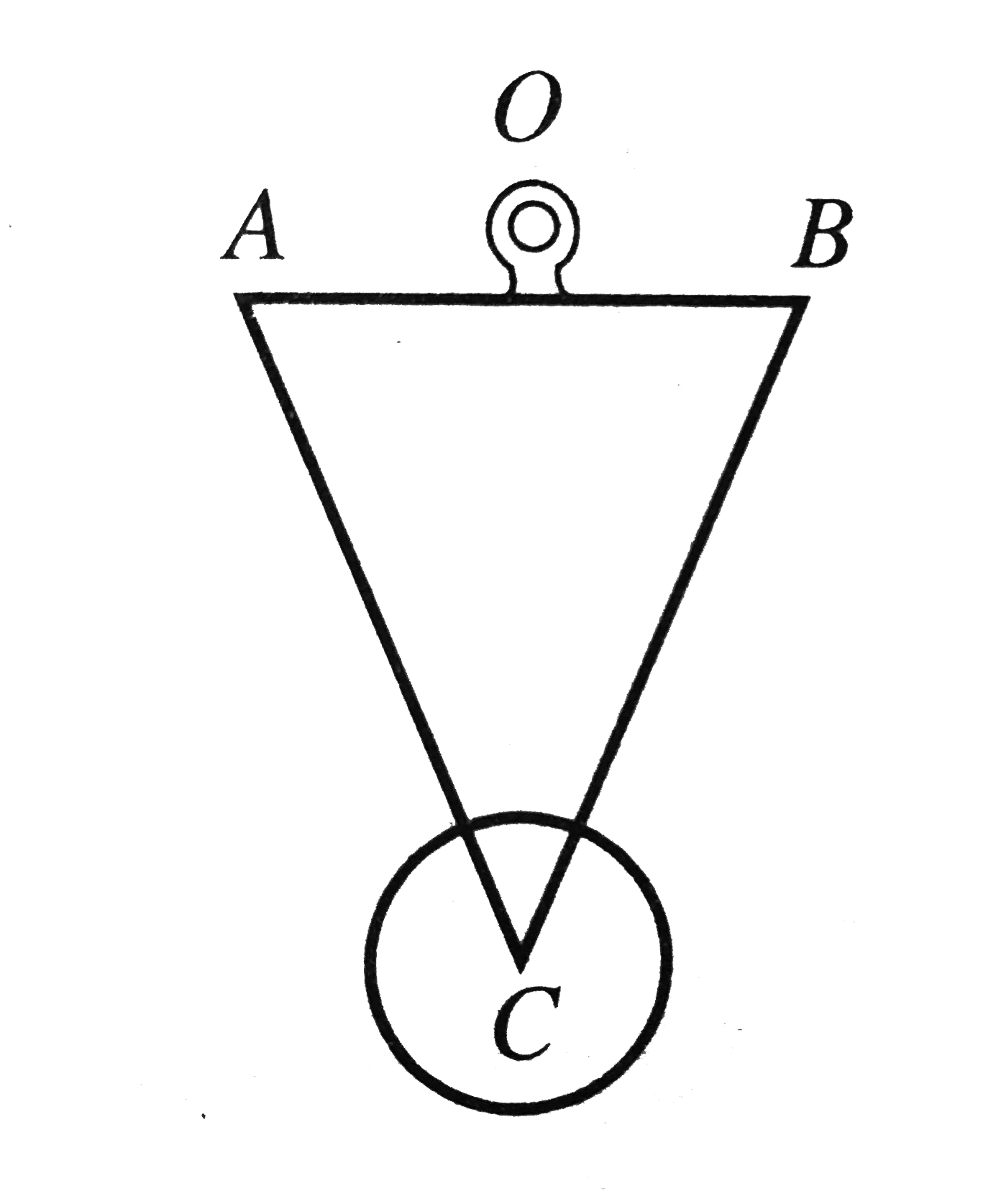
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length l1=5cm and coefficent of linar expansion α1=18×10−6 and side length l2 and coefficient of linear expansion α2=12×10−6. find l2 so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.
View SolutionTwo rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
View SolutionTwo rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionTwo rods having length l1 and l2, made of materials with the linear coefficient of expansion α1 and α2 were welded together. The equivalent coefficients of linear expansion for the obtained rod:-

View SolutionTwo different wires having lengths L1 and L2 and respective temperature coefficient of linear expansion α1 and α2 are joined end - to - end . Then the effective temperature coefficient of linear expansion is :
View Solution
