A gaseos mixture consists of equal number of moles of two ideal gases having adiabatic exponents γ1 and γ2 and molar speific heats at constant volume Cv1 and Cv2 respectively. Which of the following statements is/are correct?
Adiabatic exponent for gaseous mixture is equal to γ1+γ22
Molar specific heat at constant volume for gaseous mixture is equal to Cv1+Cv22
Molar specific heat at constant pressure for gaseous mixture is equal to Cv1+Cv2+R2
Adiabatic exponent for gaseous mixture is 1+2RCv1+Cv2
The correct Answer is:B, D
To solve the problem regarding the gaseous mixture of two ideal gases, we need to analyze the given information and derive the necessary equations step by step.
1. Understanding the Given Information:
- We have two ideal gases with equal number of moles.
- The adiabatic exponents are denoted as γ1 and γ2.
- The molar specific heats at constant volume are Cv1 and Cv2.
2. Using the Relation between Cp and Cv:
- The relationship between the specific heats is given by:
Cp−Cv=R
- For the first gas:
Cp1=Cv1+R
- For the second gas:
Cp2=Cv2+R
3. Calculating the Molar Heat Capacity at Constant Volume for the Mixture:
- Since the number of moles of both gases is equal, let n1=n2=n.
- The molar heat capacity at constant volume for the mixture can be calculated as:
Cvmix=nCv1+nCv2n+n=Cv1+Cv22
4. Calculating the Molar Heat Capacity at Constant Pressure for the Mixture:
- Using the previously calculated Cvmix:
Cpmix=Cvmix+R=Cv1+Cv22+R
5. Calculating the Adiabatic Exponent for the Mixture:
- The adiabatic exponent γmix is given by:
γmix=CpmixCvmix
- Substituting the values:
γmix=Cv1+Cv22+RCv1+Cv22=1+2RCv1+Cv2
6. Expressing Cv1 and Cv2 in terms of γ1 and γ2:
- From the relation Cv=Rγ−1:
Cv1=Rγ1−1,Cv2=Rγ2−1
7. Substituting Cv1 and Cv2 into γmix:
- Substitute these into the expression for γmix:
γmix=1+2RRγ1−1+Rγ2−1=1+2(γ1−1)(γ2−1)(γ1+γ2−2)
8. Final Expressions:
- The final expressions for Cvmix, Cpmix, and γmix are:
- Cvmix=Cv1+Cv22
- Cpmix=Cv1+Cv22+R
- γmix=1+2RCv1+Cv2
Conclusion:
After calculating the values, we can check the correctness of the statements given in the question.
- We have two ideal gases with equal number of moles.
- The adiabatic exponents are denoted as γ1 and γ2.
- The molar specific heats at constant volume are Cv1 and Cv2.
- The relationship between the specific heats is given by:
Cp−Cv=R
- For the first gas:
Cp1=Cv1+R
- For the second gas:
Cp2=Cv2+R
- Since the number of moles of both gases is equal, let n1=n2=n.
- The molar heat capacity at constant volume for the mixture can be calculated as:
Cvmix=nCv1+nCv2n+n=Cv1+Cv22
- Using the previously calculated Cvmix:
Cpmix=Cvmix+R=Cv1+Cv22+R
- The adiabatic exponent γmix is given by:
γmix=CpmixCvmix
- Substituting the values:
γmix=Cv1+Cv22+RCv1+Cv22=1+2RCv1+Cv2
- From the relation Cv=Rγ−1:
Cv1=Rγ1−1,Cv2=Rγ2−1
- Substitute these into the expression for γmix:
γmix=1+2RRγ1−1+Rγ2−1=1+2(γ1−1)(γ2−1)(γ1+γ2−2)
- The final expressions for Cvmix, Cpmix, and γmix are:
- Cvmix=Cv1+Cv22
- Cpmix=Cv1+Cv22+R
- γmix=1+2RCv1+Cv2
After calculating the values, we can check the correctness of the statements given in the question.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -IV
Explore 9 Videos
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:Exercise-3
Explore 1 Video
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -I
Explore 15 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCE ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 64 Videos
Similar Questions
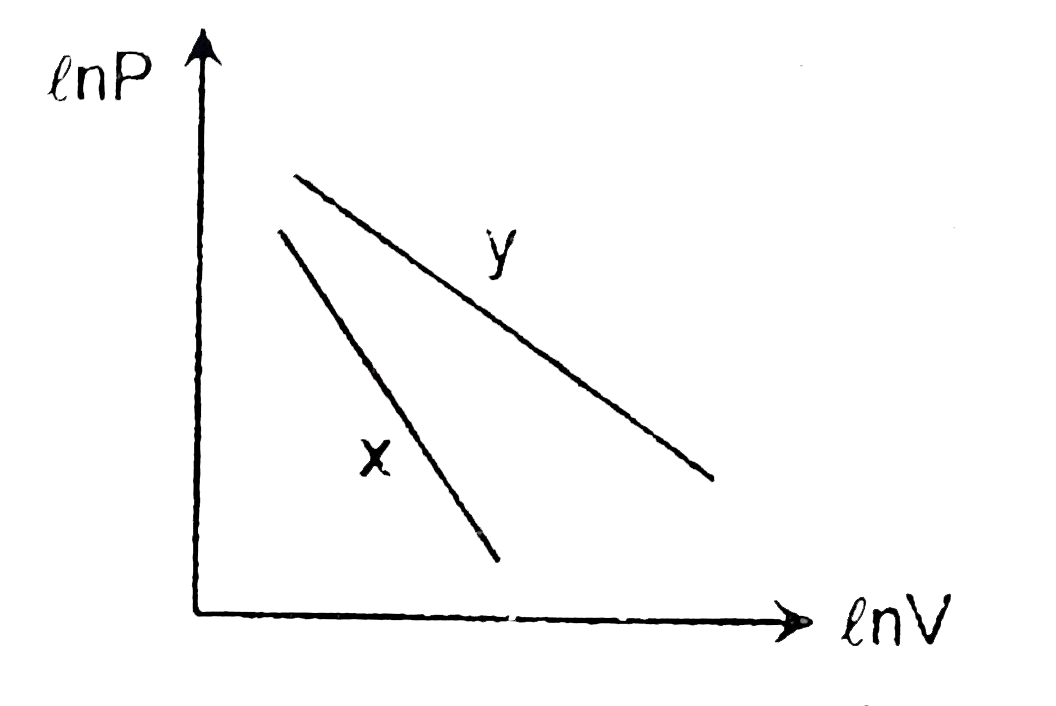
For two different gases x and y have degree of freedon f1 and f2 and molar specific heat capacities at constant volume CV1 and CV2 respectively. The lnP versus lnV graph is plotted for adiabatic process, as shown, choose the correct options.
View SolutionLet (Cv)and(Cp) denote the molar heat capacities of an ideal gas at constant volume and constant pressure respectively . Which of the following is a universal constant?
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCvandCp denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
View SolutionCalculate the specific heat capacity Cr of a gaseous mixture consisting of v1 moles of a gas of adiabatic exponent γ1 and v2 moles of another gas of adiaqbatic exponent γ2.
View Solution2 mole ideal He gas and 3 mole ideal H2 gas at constant volume find out Cv of mixture
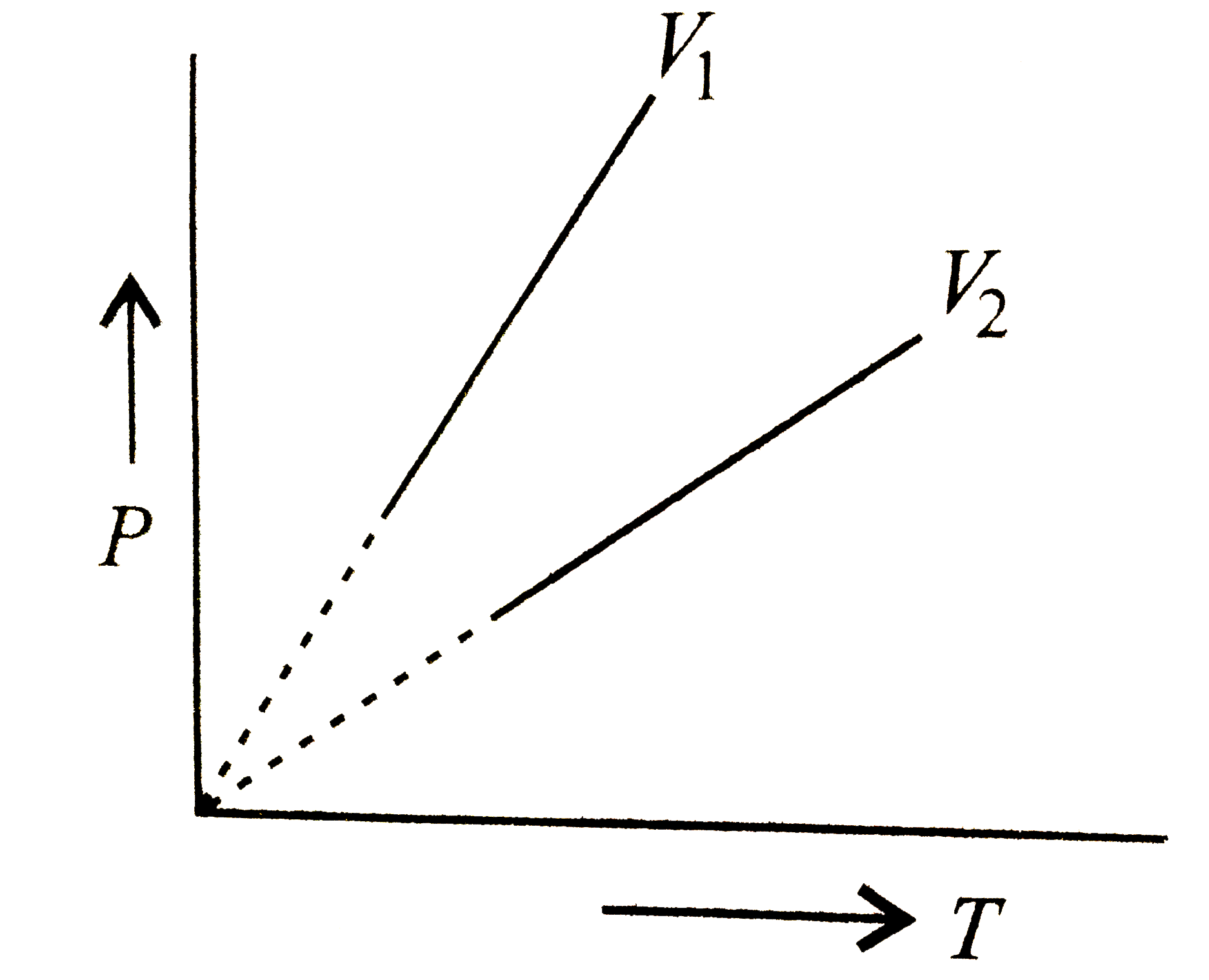
View SolutionA plot of P vs T for a given mass of gas at constant volume is a straight line . P vs T at constant volumes V1 and V2 for an ideal gas are shown below :
Which of the following is correct ?
View SolutionThe degree of freedom of mixture of two ideal gases having moles n1 and n,2 and degree of freedom f1 and f2 respectively, is
View Solution

