For a gas sample with N0 number of molecules, function N(V) is given by: N(V)=dNdV=(3N0V30)V2 for 0<V<V0 and N(V)=0 for V>V0. Where dN is number of molecules in speed range V to V+dV. The rms speed of the molecules is:
√25V0
√35V0
√2V0
√3V0
The correct Answer is:B
To find the root mean square (RMS) speed of the molecules in the given gas sample, we will follow these steps:
Step 1: Understand the given function
The function N(V) describes the distribution of molecules in a speed range. It is given by:
N(V)=dNdV=3N0V30V2for 0<V<V0
and N(V)=0 for V>V0.
Step 2: Write the expression for RMS speed
The RMS speed vrms is defined as:
vrms=
⎷∫V00v2dNN0
where dN is the number of molecules in the speed range V to V+dV.
Step 3: Substitute dN in the RMS formula
From the given function, we can express dN:
dN=N(V)dV=3N0V30V2dV
Now substituting this into the RMS speed formula:
vrms=
⎷∫V00v2(3N0V30V2dV)N0
Step 4: Simplify the expression
This simplifies to:
vrms=
⎷3N0N0V30∫V00V4dV
=
⎷3V30∫V00V4dV
Step 5: Calculate the integral
Now we need to calculate the integral ∫V00V4dV:
∫V00V4dV=(V55)V00=V505
Step 6: Substitute the integral back into the RMS formula
Substituting the result of the integral back:
vrms=
⎷3V30⋅V505
=√3V205
Step 7: Final expression for RMS speed
Thus, the final expression for the RMS speed is:
vrms=V0√35
Summary of Steps
1. Understand the distribution function N(V).
2. Write the RMS speed formula.
3. Substitute dN into the RMS formula.
4. Simplify the expression.
5. Calculate the integral ∫V00V4dV.
6. Substitute the integral back into the RMS formula.
7. Derive the final expression for vrms.
The function N(V) describes the distribution of molecules in a speed range. It is given by:
N(V)=dNdV=3N0V30V2for 0<V<V0
and N(V)=0 for V>V0.
The RMS speed vrms is defined as:
vrms=
⎷∫V00v2dNN0
where dN is the number of molecules in the speed range V to V+dV.
From the given function, we can express dN:
dN=N(V)dV=3N0V30V2dV
Now substituting this into the RMS speed formula:
vrms=
⎷∫V00v2(3N0V30V2dV)N0
This simplifies to:
vrms=
⎷3N0N0V30∫V00V4dV
=
⎷3V30∫V00V4dV
Now we need to calculate the integral ∫V00V4dV:
∫V00V4dV=(V55)V00=V505
Substituting the result of the integral back:
vrms=
⎷3V30⋅V505
=√3V205
Thus, the final expression for the RMS speed is:
vrms=V0√35
1. Understand the distribution function N(V).
2. Write the RMS speed formula.
3. Substitute dN into the RMS formula.
4. Simplify the expression.
5. Calculate the integral ∫V00V4dV.
6. Substitute the integral back into the RMS formula.
7. Derive the final expression for vrms.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:Exercise-2
Explore 1 Video
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -I
Explore 15 Videos
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -II
Explore 17 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCE ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 64 Videos
Similar Questions
Knowledge Check
If vrms is the rms speed of molecules in a gas and v is the speed of sound waves in the gas, then the ratio vrmsv is
A√3γB√γ3C√3γD√3γ
A ball is thrown downward In a viscous fluid with speed V. Terminal speed of ball is V0

View SolutionPressure of 1 mole ideal is given by
P=P0[1−12(V0V)2] V0 to 2V0. Find change in temperature.
View SolutionSpeed of sound wave in a gas V1 and rms speed of molecules of the gas at the same temperature is v2.
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
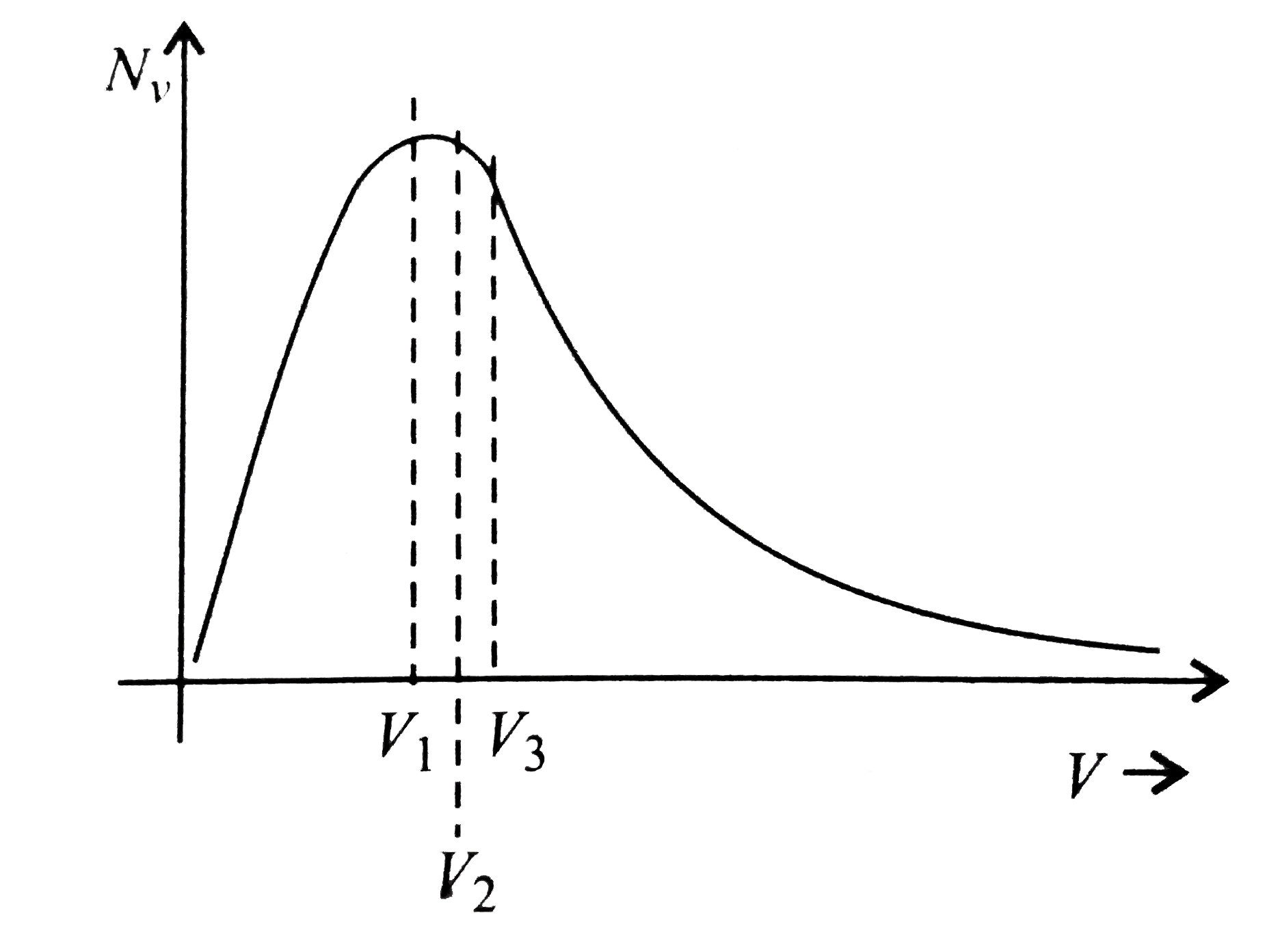
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
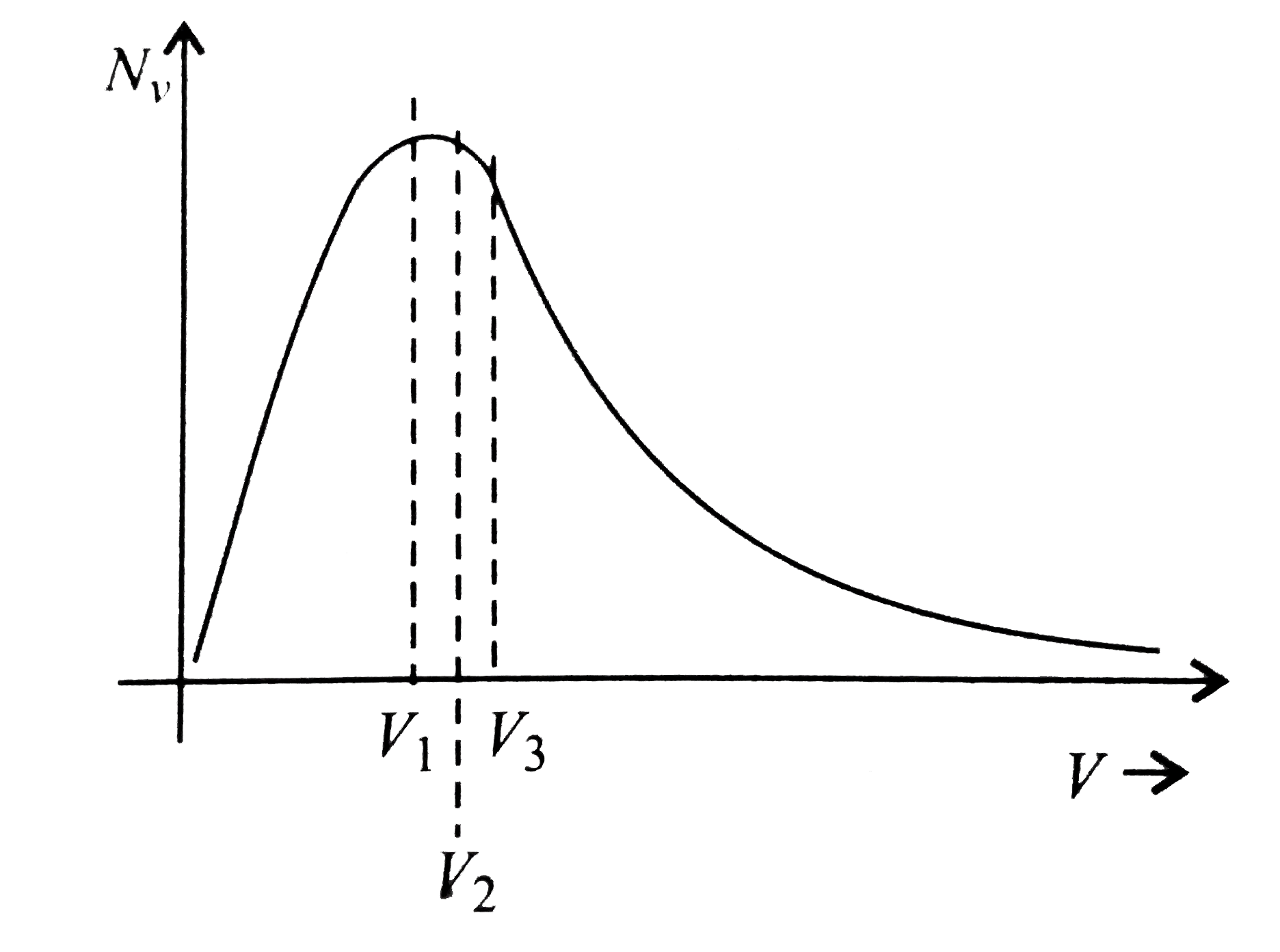
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionThe position of a particle at time t is given by the equation x(t)=V0A(1−eAt)
V0 = constant and A > 0
Dimensions of V0 and A respectively are
View SolutionPressure of 1 mole ideal gas is given by
P=P0[1−12(V0V)2] V to 2V. Find change in temperature.
View Solution

