The quantity 2UfkT represents (where U= internal energy of gas)
mass of the gas
kinetic energy of the gas
number of moles of the gas
number of molecules in the gas
The correct Answer is:D
To solve the problem, we need to analyze the expression 2UfkT where U is the internal energy of the gas, f is the degrees of freedom, k is the Boltzmann constant, and T is the temperature.
1. Understand the Internal Energy of an Ideal Gas:
The internal energy U of an ideal gas can be expressed as:
U=nFRT2
where n is the number of moles, F is the degrees of freedom, and R is the universal gas constant.
2. Substituting R with k:
We can also express the universal gas constant R in terms of the Boltzmann constant k:
R=NAk
where NA is Avogadro's number. Thus, we can rewrite the internal energy as:
U=nF(NAk)T2
3. Rearranging the Internal Energy Expression:
Simplifying the expression for U:
U=nFNAkT2
4. Finding 2UfkT:
Now, we need to compute 2UfkT:
2UfkT=2(nFNAkT2)fkT
The 2 in the numerator and denominator cancels out:
=nFNAkTfkT
5. Simplifying Further:
The kT in the numerator and denominator also cancels out:
=nFf
Since F is the degrees of freedom, the expression simplifies to:
=n
6. Conclusion:
Therefore, we find that:
2UfkT=n
This means that the quantity 2UfkT represents the number of moles of the gas.
Final Answer:
The quantity 2UfkT represents the number of moles of the gas.
The internal energy U of an ideal gas can be expressed as:
U=nFRT2
where n is the number of moles, F is the degrees of freedom, and R is the universal gas constant.
We can also express the universal gas constant R in terms of the Boltzmann constant k:
R=NAk
where NA is Avogadro's number. Thus, we can rewrite the internal energy as:
U=nF(NAk)T2
Simplifying the expression for U:
U=nFNAkT2
Now, we need to compute 2UfkT:
2UfkT=2(nFNAkT2)fkT
The 2 in the numerator and denominator cancels out:
=nFNAkTfkT
The kT in the numerator and denominator also cancels out:
=nFf
Since F is the degrees of freedom, the expression simplifies to:
=n
Therefore, we find that:
2UfkT=n
This means that the quantity 2UfkT represents the number of moles of the gas.
The quantity 2UfkT represents the number of moles of the gas.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:Exercise-2
Explore 1 Video
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -I
Explore 15 Videos
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -II
Explore 17 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCE ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 64 Videos
Similar Questions
An ideal gas can be taken form initial state 1 to final state 2 by two different process. Let ΔQ and W represent the heat given and work done by the system. Then which quantities is/are same in both process (where ΔU= internal energy of gas)
View SolutionWhat do you mean by internal energy (U) of a gas ?
View SolutionWhich of the following diagram correctly represents the variation of internal energy (U) of gas under expansion at constant temperature.
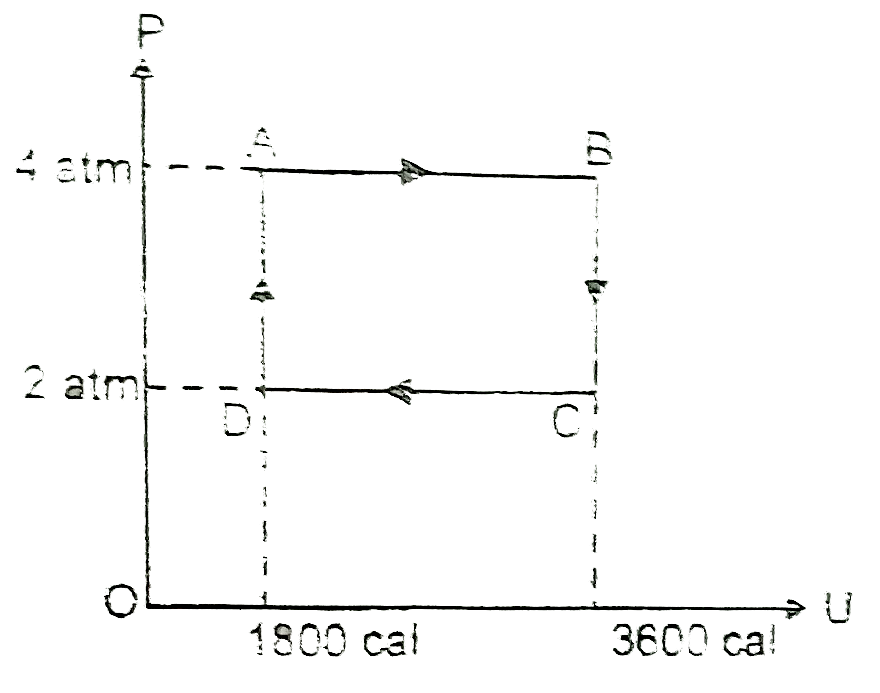
View SolutionTwo moles of an ideal monoatomic gas undergo a cyclic process which is indicated on a P−U diagram, where U is the internal energy of the gas. The work done by the gas in the cycle is k×102In2. Find k.
View SolutionThe given (p - U) graph shows the variation of internal energy of an ideal gas with increase in pressure. Which of the following pressure - volume graph is equivalent to this graph ?
 .
.
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionAn ideal gas is taken from state 1 to state 2 through optional path A,B,CandD as shown in the PV diagram. Let Q,WandU represent the heat supplied, work done and change in internal energy of the gas respectively.
Then,

View SolutionAssertion: Under adiabatic free expansion, (dUdV)T is +ve when attractive forces are dominant between gas molecules [U,V,T respresent internal energy, volume and temperature of gas respectively]
Reason: Internal energy is a state function.
View SolutionAn ideal monoatomic gas undergoes a process in which its internal energy U and density ρ vary as Uρ= constant. The ratio of change in internal energy and the work done by the gas is
View Solution

