Considering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law to include the term due to displacment current.

Ampere's law is bound to fail for nonsteady current, which can be seen with the help of charging up of capacitor ∮→B.d→l=μ0lenc (Ampere's Law) now, we want to apply it to the amperian loop shown in diagram. How do we determine lenc it is the total current piercing a surface that has the loop for its boundary. In this case, the wire punctures this sucface so lenc=l, fine but what if l draw insttead the balloon shaped surface. NO current passes through this surface and l conclude that lenc=0
ϕE=EA=qinε0
So we can conclude there is a missing term in Ampere's circuital law, that is known as displacement current.
id=dQindt=ddt(ϕEε0)=ε0ddt(ϕE)
So total current i=ic+id=ic+ε0ddt(ϕE)
Topper's Solved these Questions
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 2
Explore 6 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
Similar Questions
Two circular plates of radius 0.1m are used to from a parallel plate capacitor. If displacement current between the plates is 2π.ampere, then find m agnetic filed produced by displacement current 4 cm from the axis of the plates.
View SolutionConsider a parallel plate capacitor is charged by a constant current I, with plate area A and separation between the plates d. Consider a plane surface of area A/4 parallel to the plates and drawn symmetrically between the plates. Find the displacement current through this area.
View Solution
Knowledge Check
The charge on a parallel plate capacitor varies as q=q0cos2πt. The plates are very large and close together (area = A, separation = d). The displacement current through the capacitor is
Aq02πυsinπυtB−q02πυsin2πυtCq02πsinπυtDq0πυsin2πυt
A parallel plate capacitor is charged to 60μC. Due to a radioactive source, the plate losses charge at the rate of 1.8×10−8Cs−1. The magnitued of displacement current is
View SolutionA parallel plate capacitor is charged to 60μC. Due to a radioactive source, the plate losses charge at the rate of 1.8×10−8Cs−1. The magnitued of displacement current is
View SolutionA parallel - plate capacitor is being charged.Show that the displacement current across an area in the region between the plates and parallel to it is equal to the conduction current in the connecting wires.
View SolutionA parallel - plate capacitor is being charged.Show that the displacement current across an area in the region between the plates and parallel to it is equal to the conduction current in the connecting wires.
View SolutionTwo circular plates of radius 0.1 m are used to form a parallel capacitor. If displacement current between the plates is 2π ampere, then find magnetic produced by displacement current 4 cm from the axis of the plates.
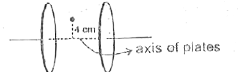
View SolutionA parallel plate capacitor of plate separation 2 mm is connected in an electric circuit having source voltage 400V. If the plate area is 60 cm2, then the value of displacement current for 10−6 sec. will be
View SolutionA large parallel plate capacitor, whose plates have an area of 1m2 and are separated from each other by 1 mm, is being charged at a rate of 25Vs−1 . If the dielectric constant 10, then the displacement current at this instant is
View Solution

