As shown in the figure AB is a rod of length 30 cm and area of cross section 1.0 am2 and thermal conductivity 336 SI units. The ends A and B are maintained at temperature20∘Cand40∘C respectively. A point C of this rod is connected to a box D, containing ice at 0∘C through a highly conducting wire of negligible heat capacity. The rate at which ice melts in the box is : (Assume latent heat of fusion for ice Lf=80cal/g)
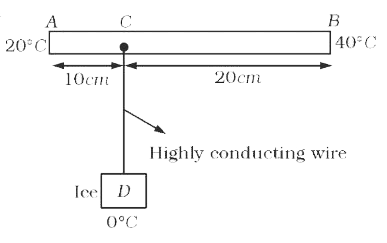
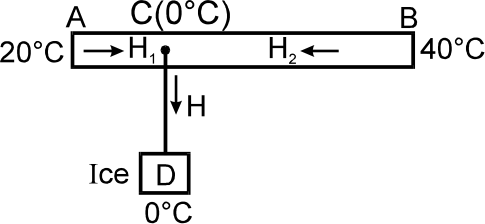
Thermal resistance of AC (=LKA)=0.1336×1×10−4=103336=R (suppose)
thermal resistance of BC =0.2336×10−4=2R
∴H1=20R,H2=402R=20R
∴H=H1+H2=40R=40×336103=13440103=13.44 watt
Rate of melting of ice =HLf=13.44/4.280g/s=40mg/s
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100^@C . At the other end large quantity of ice is kept at 0^@C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice. .
View Solution
As shown in Fig. AB is rod of length 30 cm and area of cross section 1.0cm2 and thermal conductivity 336 SI units. The ends A and B are maintained at temperatures 20∘C and 40∘C, respectively .A point C of this rod is connected to a box D, containing ice at 0∘C through a highly conducting wire of negligible heat capacity. The rate at which ice melts in the box is (assume latent heat of fusion for ice Lf=80cal/g)
View SolutionOne end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View SolutionTwo rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80^(@)C and the end D is maintained at 10^(@)C , calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y .
View SolutionOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
View SolutionThree conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at 20^(@)C, 90^(@)C and 0^(@)C . The ratio of lengths BD and BC if there is no heat flow in AB is
View SolutionOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at 100° C. If the other end of the rod is maintained at 0°C, the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100 W/m-K)
View SolutionA cylindrical rod of 50 cm length and having 1 cm^(2) cross sectional area isused as a conducting material between an ice bath at 0^(@)C and a vacuum chamber at 27^(@)C as shown in figure. The end of rod which is inside the vacuum chamber behaves like a black body and is at temperature 17^(@)C in steady state. Find the thermal conductivity of the material of rod and rate at which ice is melting in the ice bath. Given that latent heat of fusion of ice is 3.35 xx l0^(5) J//kg ..
View SolutionOne end of 0.5 m long metal rod is in steam at 100∘C and the other end is put in ice at 0∘C. If ice melts at the rate of 10 g/min, calculate the thermal conductivity of the metal. Take, cross sectional area of rod=2πcm2 . Latent ice of heat = 80 cal/g
View SolutionThree rods AB, BC and AC having thermal resistances of 10 units, 10 units and 20 units, respectively, are connected as shown in the figure. Ends A and C are maintained at constant temperatures of 100^@C and 0^@C , respectively. The rate at which the heat is crossing junction B is
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is

View SolutionA rod of negligible heat capacity has length 20 cm, area of cross--section 1.0 cm2 and thermal conductivity 200 W/m−0C. The temperature of one end is maintained at 00C and that of the other end is slowly and linearly varied from 00C to 600C in 10 minutes. Assuming no loss of heat through the sides. The total heat transmitted through the rod in these 10 minutes is x×600. Find x
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100^@C . At the other end large quantity of ice is kept at 0^@C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice. .
View SolutionOne end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View Solution

