If specific ehat capacity of a substance in solid and liquid state is proportional to temperature of the substance, then if heat is supplied to the solid intially at −20∘C (having melting 0∘C) at contant rate. Then the temperature dependence of solid with time will be best represented by:
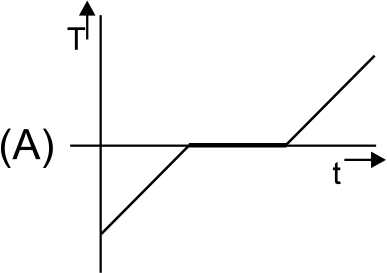
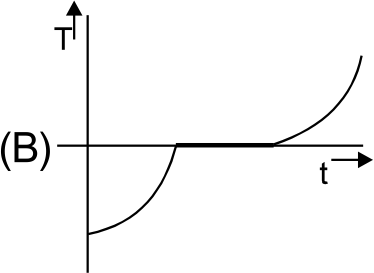
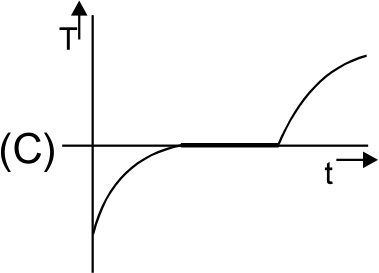
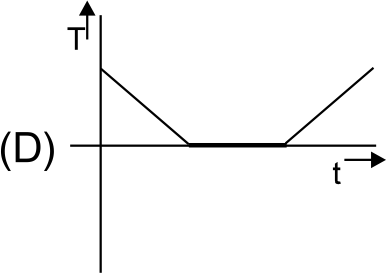
To solve the problem, we need to analyze how the temperature of a solid substance changes over time when heat is supplied at a constant rate, given that the specific heat capacity of the substance is proportional to its temperature.
1. Understanding the Problem:
- We have a solid substance at an initial temperature of -20°C.
- The melting point of the substance is 0°C.
- The specific heat capacity (C) is proportional to the temperature (T), i.e., C=kT where k is a constant.
2. Heat Supplied:
- Let P0 be the constant rate at which heat is supplied.
- The amount of heat supplied in a small time interval dt is dq=P0dt.
3. Relating Heat to Temperature Change:
- The change in heat can also be expressed as:
dq=m⋅C⋅dT=m⋅kT⋅dT
- Here, m is the mass of the substance.
4. Setting Up the Equation:
- Equating the two expressions for dq:
P0dt=m⋅kT⋅dT
- Rearranging gives:
dTT=P0m⋅kdt
5. Integrating Both Sides:
- Integrate both sides from the initial temperature Ti=−20°C to Tf and from t=0 to t:
∫Tf−201TdT=P0m⋅k∫t0dt
- This results in:
ln|Tf|−ln|−20|=P0m⋅kt
- Simplifying gives:
ln(Tf−20)=P0m⋅kt
6. Exponentiating:
- Exponentiating both sides:
Tf−20=eP0m⋅kt
- Thus,
Tf=−20eP0m⋅kt
7. Behavior of Temperature Over Time:
- As time increases, Tf increases exponentially until it reaches the melting point (0°C). After reaching 0°C, the heat will be used for the phase change (melting) rather than increasing temperature.
Conclusion:
The temperature dependence of the solid with time will be best represented by an exponential function until the melting point is reached, after which it will remain constant during the phase change.
- We have a solid substance at an initial temperature of -20°C.
- The melting point of the substance is 0°C.
- The specific heat capacity (C) is proportional to the temperature (T), i.e., C=kT where k is a constant.
- Let P0 be the constant rate at which heat is supplied.
- The amount of heat supplied in a small time interval dt is dq=P0dt.
- The change in heat can also be expressed as:
dq=m⋅C⋅dT=m⋅kT⋅dT
- Here, m is the mass of the substance.
- Equating the two expressions for dq:
P0dt=m⋅kT⋅dT
- Rearranging gives:
dTT=P0m⋅kdt
- Integrate both sides from the initial temperature Ti=−20°C to Tf and from t=0 to t:
∫Tf−201TdT=P0m⋅k∫t0dt
- This results in:
ln|Tf|−ln|−20|=P0m⋅kt
- Simplifying gives:
ln(Tf−20)=P0m⋅kt
- Exponentiating both sides:
Tf−20=eP0m⋅kt
- Thus,
Tf=−20eP0m⋅kt
- As time increases, Tf increases exponentially until it reaches the melting point (0°C). After reaching 0°C, the heat will be used for the phase change (melting) rather than increasing temperature.
The temperature dependence of the solid with time will be best represented by an exponential function until the melting point is reached, after which it will remain constant during the phase change.
Topper's Solved these Questions
Similar Questions
State whether the specific heat capacity of a substance remains the same when its state changes from solid to liquid.
View SolutionDensity of solids hardly changes with a rise in temperature by 20∘C.
View SolutionThe process due to which a solid changes into liquid state at some fixed temperature by absorption of heat energy is known as
View Solution
Heat is supplied to a certain homogeneous sample of matter, at a uniform rate. Its temperature is plotted against time, as shown Which of the following conclusions can be drawn?
(i) Its specific heat capacity is greater in the solid state than the liquid state.
(ii) Its specific heat capacity is greater in the liquid state than in the solid state.
(iii) Its latent heat of vaporization is greater than its latent heat of fusion.
(iv) Its latent heat of vaporization is smaller than its latent heat of fusion
View SolutionA solid material is supplied heat at a constant rate. The temperature of material is changing with heat input as shown in the figure. What does the slope of DE represent ?

View SolutionThe quantity of heat required to change the unit mass of a solid substance, from solid-state to liquid state, while the temperature remains constant, is known as
View SolutionA well insulated substance in solid state is heated at a constant rate until it vaporizes completely. The temperature-time graph of the substance is shown below . Which of the following statements is//are true?
_E01_077_Q01.png)
View SolutionState which expands more, when heated to the same temperature : solid, liquid or gas ?
View Solution200gm water is filled in a calorimetry of negligible heat capacity. It is heated till its temperature is increase by 20∘C. Find the heat supplied to the water.
View SolutionA substance is in the solid from at 0∘C. The amount of heat added to this substance and its temperature is plotted in the graph . The specific heat capacity of the solid substance is 0.5cal//g∘C.
_E01_233_Q01.png)
The mass of the substance is -
View Solution

