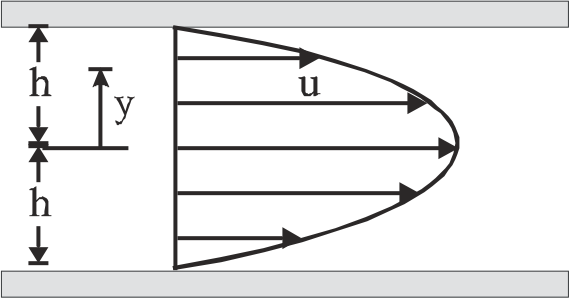
The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
![The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation u=(3V)/2[1-(y/h)^(2)] where V is the mean velocity. The fluid has coefficient of viscosity eta Answer the following 3 questions for this situation. Consider a rectangular cross section of dimensions l x 2h as shown. The side AB is parallel to the plates. Volume flow rate through this cross section is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_07_E01_041_Q01.png)
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Consider a rectangular cross section of dimensions l x 2h as shown. The side AB is parallel to the plates. Volume flow rate through this cross section is
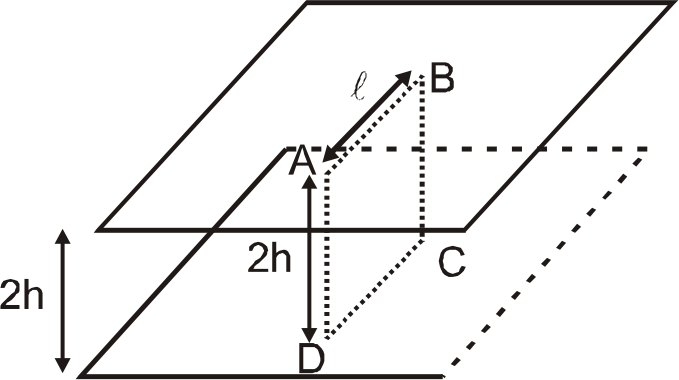
lhV/2
lhV
2lhV
3lhV
For this type of parallel flow the shearing stress is given as ta=ηdudy....(i)
For the given distribution
dudy=−3Vyh2....(ii)
(a) Along the bottom wall so that (from eq. (ii))
dudy=3Vh and therefore the shearing stress is τbottom wall=η(3Vh)
(b) Along the plane where y=h/2 it follows from equation (ii) that
dudy=−3Vyh2 and thus the shearing stress is |τ|=η3V2h.
(C) 
Rate of volume flow
2∫h03V2(1−y2h2)dy.l=2Vlh
Topper's Solved these Questions
Similar Questions
The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Shear stress acting on the bottom wall is
View SolutionCheck the correctness of the equation v=Kηrρ using dimensional analysis, where v is the critical velocity η is the coefficient of viscosity, r is the radius and ρ is the density?
View SolutionAn ideal fluid flows through a pipe of circular cross - section with diameters 5 cm and 10 cm as shown in the figure. The ratio of velocities of fluid at A and B is

View SolutionThe equation of a wave is given by Y=Asinω(xv−k), where ω is the angular velocity and v is the linear velocity. Find the dimension of k.
View SolutionA liquid having coefficient of viscosity 0.02 decapoise is filled in a container of cross-sectional area 20 m^2 viscous drag between two adjacent layers in flowing is 1 N, then velocity gradient is
View SolutionThe coefficient of viscosity (η) of a fluid moving steadily between two surface is given by the formula (f)=ηAdV/dx where f is the frictional force on the flluid, A is the area in the fluid, and dN/dx is velocity gradient inside the fluid at that area. The SI unit of viscosity is given as :
View SolutionA square plate of 1m side moves parallel to a second plate with velocity 4m/s. A thin layer of water exist between plates. If the viscous force is 2N and the coefficient of viscosity is 0.01 poise then find the distance between the plates in mm.
View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionThe equation of a wave is given by
y=asinω[xv−k]
where ω is angular velocity and v is the linear velocity . The dimensions of k will be
View SolutionThe equation of a wave is given by
y=asinω[xv−k]
where ω is angular velocity and v is the linear velocity . The dimensions of k will be
View Solution
