Consider two infinite large parallel current carrying sheet. Current unit width in both sheets is 1√πA/m. If direction of current in both sheets is same than force per unit area on each sheet will be :
10−7N/m2
0.5×10−7N/m2
2×10−7N/m2
10−5N/m2
To solve the problem of finding the force per unit area on each sheet due to the magnetic field created by the other sheet, we can follow these steps:
Step 1: Understand the Magnetic Field due to a Current-Carrying Sheet
For an infinite sheet carrying a current density k (current per unit width), the magnetic field B produced by the sheet is given by the formula:
B=μ0k2
where μ0 is the permeability of free space.
Step 2: Calculate the Magnetic Field from One Sheet
Given that the current density k=1√πA/m, we can substitute this value into the formula for the magnetic field:
B=μ0(1√π)2
Step 3: Determine the Direction of the Magnetic Field
Since both sheets carry current in the same direction, the magnetic field produced by each sheet will be in the same direction between the sheets.
Step 4: Calculate the Force per Unit Area on One Sheet
The force per unit area (pressure) P on a current-carrying conductor in a magnetic field is given by:
P=B⋅k
Substituting the expression for B:
P=(μ0k2)⋅k=μ0k22
Step 5: Substitute the Values
Now we substitute k=1√π into the equation:
P=μ0(1√π)22=μ0⋅1π2
Step 6: Substitute the Value of μ0
The permeability of free space μ0 is approximately 4π×10−7T m/A. Thus,
P=4π×10−7⋅1π2=4×10−72=2×10−7N/m2
Conclusion
The force per unit area on each sheet is:
P=2×10−7N/m2
Final Answer
The force per unit area on each sheet is 2×10−7N/m2.
---
For an infinite sheet carrying a current density k (current per unit width), the magnetic field B produced by the sheet is given by the formula:
B=μ0k2
where μ0 is the permeability of free space.
Given that the current density k=1√πA/m, we can substitute this value into the formula for the magnetic field:
B=μ0(1√π)2
Since both sheets carry current in the same direction, the magnetic field produced by each sheet will be in the same direction between the sheets.
The force per unit area (pressure) P on a current-carrying conductor in a magnetic field is given by:
P=B⋅k
Substituting the expression for B:
P=(μ0k2)⋅k=μ0k22
Now we substitute k=1√π into the equation:
P=μ0(1√π)22=μ0⋅1π2
The permeability of free space μ0 is approximately 4π×10−7T m/A. Thus,
P=4π×10−7⋅1π2=4×10−72=2×10−7N/m2
The force per unit area on each sheet is:
P=2×10−7N/m2
The force per unit area on each sheet is 2×10−7N/m2.
Topper's Solved these Questions
Similar Questions
Two parallel wires are carrying electric currents of equal magnitude and in the same direction. They
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View Solution
Knowledge Check
The two linear parallel conductors carrying currents in the opposite direction…………………each other.
AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
The magnetic field midway between two parallel current carrying wires, carrying currents I and 2i in same direction is B. If the current in the wire with current I is switched off, the magnetic field will become
View SolutionFour infinite thin current carrying sheets are placed in Y-Z plane. The 2D view of the arrangement is as shown in Fig. Direction of current has alos been shown in the figure. The linear current density, i.e., current per unit width in the four sheets are I, 2I, 3I, and 4I, respectively.

View Solutionin given figure X and Y are two long straight parallel conductor each carrying a current 2 A. the force per unit length on each conductor is F. when the current in each is changed to 1 A and reversed in direction. the force per unit length on each is now

View SolutionUsing the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current.
View SolutionTwo infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
View SolutionA large metal sheet carries an electric current along its surface. Current per unit length is λ . Magnetic field near the metal sheet is.

View SolutionFigure shows cross section of two large parallel metal sheets carrying electric currents along their surface. The current in each sheet is 10/πA/m along the width, Consider two points A and B, as shown in the figure with their positions.
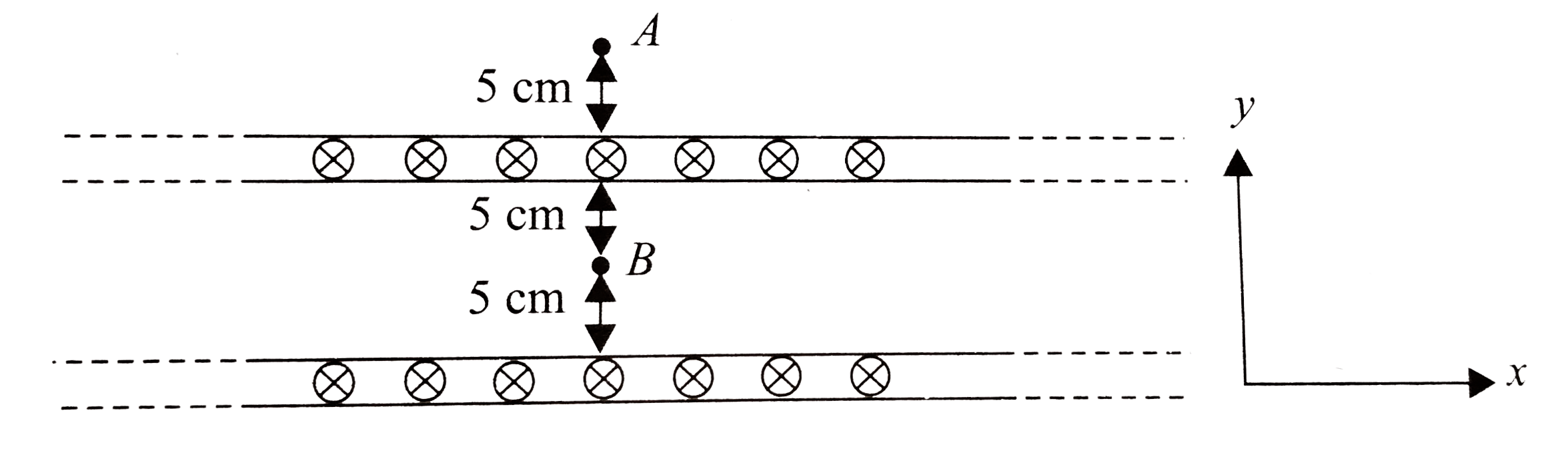
View Solution