Chords AB and CD of a circle when extended meet at point X. Given AB =4 cm, BX=6 cm and XD=6cm, calculate the length of CD.
The correct Answer is:7cm
To solve the problem step by step, we will use the intersecting chords theorem, which states that if two chords intersect each other, the products of the lengths of the segments of each chord are equal.
1. Identify the Given Lengths:
- Chord AB = 4 cm
- Segment BX = 6 cm
- Segment XD = 6 cm
- Let the length of chord CD be represented as x.
2. Determine the Length of AX:
- Since AB = 4 cm and BX = 6 cm, we can find AX:
AX=AB+BX=4cm+6cm=10cm
3. Set Up the Equation Using the Intersecting Chords Theorem:
- According to the theorem:
AX⋅BX=CX⋅DX
- We know:
- AX=10cm
- BX=6cm
- CX=x (the part of CD we want to find)
- DX=6cm
- Therefore, we can write:
10⋅6=x⋅6
4. Simplify the Equation:
- This simplifies to:
60=6x
5. Solve for x:
- Divide both sides by 6:
x=606=10cm
6. Calculate the Length of CD:
- Since CD consists of CX and DX:
CD=CX+DX=x+6=10+6=16cm
Final Answer:
The length of CD is 16 cm.
- Chord AB = 4 cm
- Segment BX = 6 cm
- Segment XD = 6 cm
- Let the length of chord CD be represented as x.
- Since AB = 4 cm and BX = 6 cm, we can find AX:
AX=AB+BX=4cm+6cm=10cm
- According to the theorem:
AX⋅BX=CX⋅DX
- We know:
- AX=10cm
- BX=6cm
- CX=x (the part of CD we want to find)
- DX=6cm
- Therefore, we can write:
10⋅6=x⋅6
- This simplifies to:
60=6x
- Divide both sides by 6:
x=606=10cm
- Since CD consists of CX and DX:
CD=CX+DX=x+6=10+6=16cm
The length of CD is 16 cm.
Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
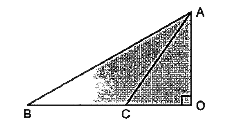
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

View SolutionChords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionAB and CD are two chords of a circle intersecting at a point P inside the circle. If
AP=3cm, PB= 2.5cm and CD= 6.5 cm, determine CP.
View SolutionAB and CD are two chords of a circle intersecting at a point P inside the circle. If
AB= 24cm, AP= 4cm and PD = 8cm, determine CP
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.
View SolutionTwo chords AB and CD of a circle are each at distances 4 cm from the centre. Then,
View SolutionIn the figure, given below X and Y are the mid-points of AB and AC respectively. Given that BC = 6 cm, AB = 5-4 cm and AC = 5-0 cm, calculate the perimeter of trapezium YXBC.

View Solution
