The points A, B and Care (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC.
If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
The correct Answer is:
To solve the problem step by step, we will find the equations of lines AB and BC, and then determine the coordinates of points P and Q where these lines intersect the y-axis and x-axis, respectively.
Step 1: Find the equation of line AB
Given points:
- A(4, 0)
- B(2, 2)
Calculate the slope (m) of line AB:
m=y2−y1x2−x1=2−02−4=2−2=−1
Using the point-slope form of the line equation:
y−y1=m(x−x1)
Using point A(4, 0):
y−0=−1(x−4)
y=−x+4
Rearranging to standard form:
x+y=4
Step 2: Find the equation of line BC
Given points:
- B(2, 2)
- C(0, 6)
Calculate the slope (m) of line BC:
m=y2−y1x2−x1=6−20−2=4−2=−2
Using the point-slope form of the line equation:
Using point C(0, 6):
y−6=−2(x−0)
y−6=−2x
y+2x=6
Step 3: Find the coordinates of point P where line AB cuts the y-axis
To find the y-intercept (P), set x=0 in the equation of line AB:
0+y=4⟹y=4
Thus, the coordinates of point P are:
P(0,4)
Step 4: Find the coordinates of point Q where line BC cuts the x-axis
To find the x-intercept (Q), set y=0 in the equation of line BC:
0+2x=6⟹2x=6⟹x=3
Thus, the coordinates of point Q are:
Q(3,0)
Final Answer:
- The equation of line AB is x+y=4.
- The equation of line BC is y+2x=6.
- The coordinates of point P are (0,4).
- The coordinates of point Q are (3,0).
- A(4, 0)
- B(2, 2)
m=y2−y1x2−x1=2−02−4=2−2=−1
y−y1=m(x−x1)
Using point A(4, 0):
y−0=−1(x−4)
y=−x+4
x+y=4
- B(2, 2)
- C(0, 6)
m=y2−y1x2−x1=6−20−2=4−2=−2
Using point C(0, 6):
y−6=−2(x−0)
y−6=−2x
y+2x=6
0+y=4⟹y=4
Thus, the coordinates of point P are:
P(0,4)
0+2x=6⟹2x=6⟹x=3
Thus, the coordinates of point Q are:
Q(3,0)
- The equation of line AB is x+y=4.
- The equation of line BC is y+2x=6.
- The coordinates of point P are (0,4).
- The coordinates of point Q are (3,0).
Topper's Solved these Questions
- EQUATION OF A LINEBook:ICSEChapter:EQUATION OF A LINEExercise:EXERCISE 14(E)
Explore 68 Videos
- EQUATION OF A LINEBook:ICSEChapter:EQUATION OF A LINEExercise:EXERCISE 14(C)
Explore 32 Videos
- CYLINDER, CONE AND SPHERE Book:ICSEChapter:CYLINDER, CONE AND SPHERE Exercise:EXERCISE 20 (G)
Explore 23 Videos
- FACTORISATIONBook:ICSEChapter:FACTORISATIONExercise:M.C.Q(Competency Based Questions )
Explore 15 Videos
Similar Questions
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. AB produced cuts the y-axis at P and CB produced cuts the x-axis at Q. Find the co-ordinates of the points P and Q. Find the equation of the straight line joining the mid-points of Ac and OB (where O is the origin), and verify that this line passes through the mid- point of PQ.
View SolutionThe co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
the equation of PQ
View SolutionThe line through P(5, 3) intersects y-axis at Q.
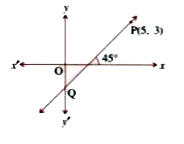
Find the co-ordinates of Q.
View SolutionThe co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
the gradient of PQ.
View SolutionPoints A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image :
A" of A under reflection in the y-axis.
View SolutionPoints A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image :
A' of A under reflection in the x-axis.
View SolutionP and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P' and Q in the y-axis to Q'. State the co-ordinates of P' and 'Q .
View SolutionThe line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
the co-ordinates of A and B.
View SolutionPoints A and B have the co-ordinates (−2,4)and(−4,1) respectively. Find:
the co-ordinates of B', the image of B in y-axis.
View SolutionThe equation of a line is 3x−4y+12=0. It meets the x-axis at point A and the y-axis at point B. Find :
the co-ordinates of points A and B.
View Solution