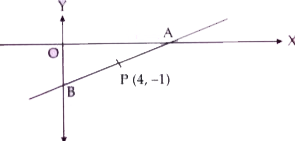A line AB meets the x-axis at A and the y-axis at B. P(4,-1) divides AB in the ratio 1:2
(i) Write down the co-ordinates of A and B.
(ii)find the equation of the line through p and perpendicular to AB

The correct Answer is:A=(6,0);B=(0,4)andarea=12sq.cm
Step by step video, text & image solution for A line AB meets the x-axis at A and the y-axis at B. P(4,-1) divides AB in the ratio 1:2 (i) Write down the co-ordinates of A and B. (ii)find the equation of the line through p and perpendicular to AB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- EQUATION OF A LINEBook:ICSEChapter:EQUATION OF A LINEExercise:EXERCISE 14(E)
Explore 68 Videos
- EQUATION OF A LINEBook:ICSEChapter:EQUATION OF A LINEExercise:EXERCISE 14(C)
Explore 32 Videos
- CYLINDER, CONE AND SPHERE Book:ICSEChapter:CYLINDER, CONE AND SPHERE Exercise:EXERCISE 20 (G)
Explore 23 Videos
- FACTORISATIONBook:ICSEChapter:FACTORISATIONExercise:M.C.Q(Competency Based Questions )
Explore 15 Videos
Similar Questions
Knowledge Check
The line xa−yb=1 cuts the x-axis at P. The equation of the line through P and perpendicular to the given line is
A(a) x+y=abB(b) x+y=a+bC(c) ax+by=a2D(d) bx+ay=b2
A line AB meets X-axis at A and Y-axis at B. P(4,−1) divides AB in the ratio 1:2.
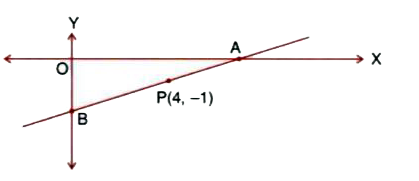
Find the Coordinates of A and B
View SolutionA line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1:2.
(ii) Find the equation of the line through P and perpendicular to AB
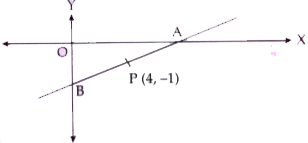
View SolutionA line AB meets the x-axis at point A and y-axis at point B. The point P(-4,-2) divides the line segment AB internally such that AP : PB = 1:2. Find :
equation of line through P and perpendicular to AB.
View SolutionThe line segment joining the points A (3,-4) and B (-2, 1) is divided in the ratio 1:3 at point P in it. Find the co-ordinates of P.
Also, find the equation of the line through P and perpendicular to the line 5x–3y=4.
View SolutionThe line 4x−3y+12=0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x−3y+12=0.
View SolutionWrite down the equation of the line AB, through (3, 2) and perpendicular to the line 2y=3x+5.
View SolutionA line 5x+3y+15=0 meets y-axis at point P. Find the co-ordinates of point P. Find the equation of a line through P and perpendicular to x−3y+4=0.
View Solution