In ΔABC,D is mid-point of AB and E is
mid -point of BC. Calculate
(i) DE if AC = 6.4 cm,
(ii) ∠DEB if ∠ACB=63∘
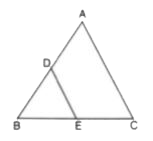
The correct Answer is:3.2cm
(ii) 63∘
Step by step video, text & image solution for In Delta ABC, D is mid-point of AB and E is mid -point of BC. Calculate (i) DE if AC = 6.4 cm, (ii) angle DEB " if " angle ACB = 63^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
- BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - RECTILINEAR FIGURES4videos
CHAPTER REVISION (STAGE 2)
- BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - CONSTRUCTIONS OF POLYGONS19videos
CHAPTER REVISION (STAGE 2)
- BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - INEQUALITIES5videos
CHAPTER REVISION (STAGE 2)
- BOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )22videos
AREA THEOREMS
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution10videos
CHAPTERWISE REVISION (STAGE 1)
Similar Questions
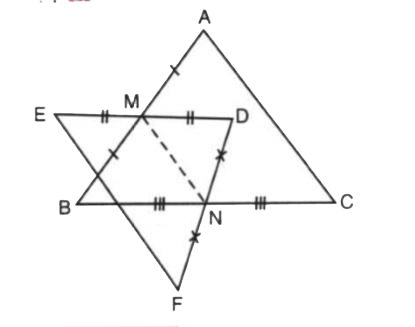
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
 View Solution
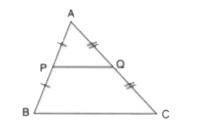
View SolutionIn triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 , find the perimeter of the trapezium PBCQ.
 View Solution
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYBView SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14area of△ABC. GIVEN : A △ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionIn triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
View SolutionIn ΔABC, E is mid-point of side AB and EBCD is a parallelogram. If the area of ΔABC is 80 cm, find the area of parallelogram EBCD.
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect ∠ADC and
(iii) Angle DEC is a right angle.View Solution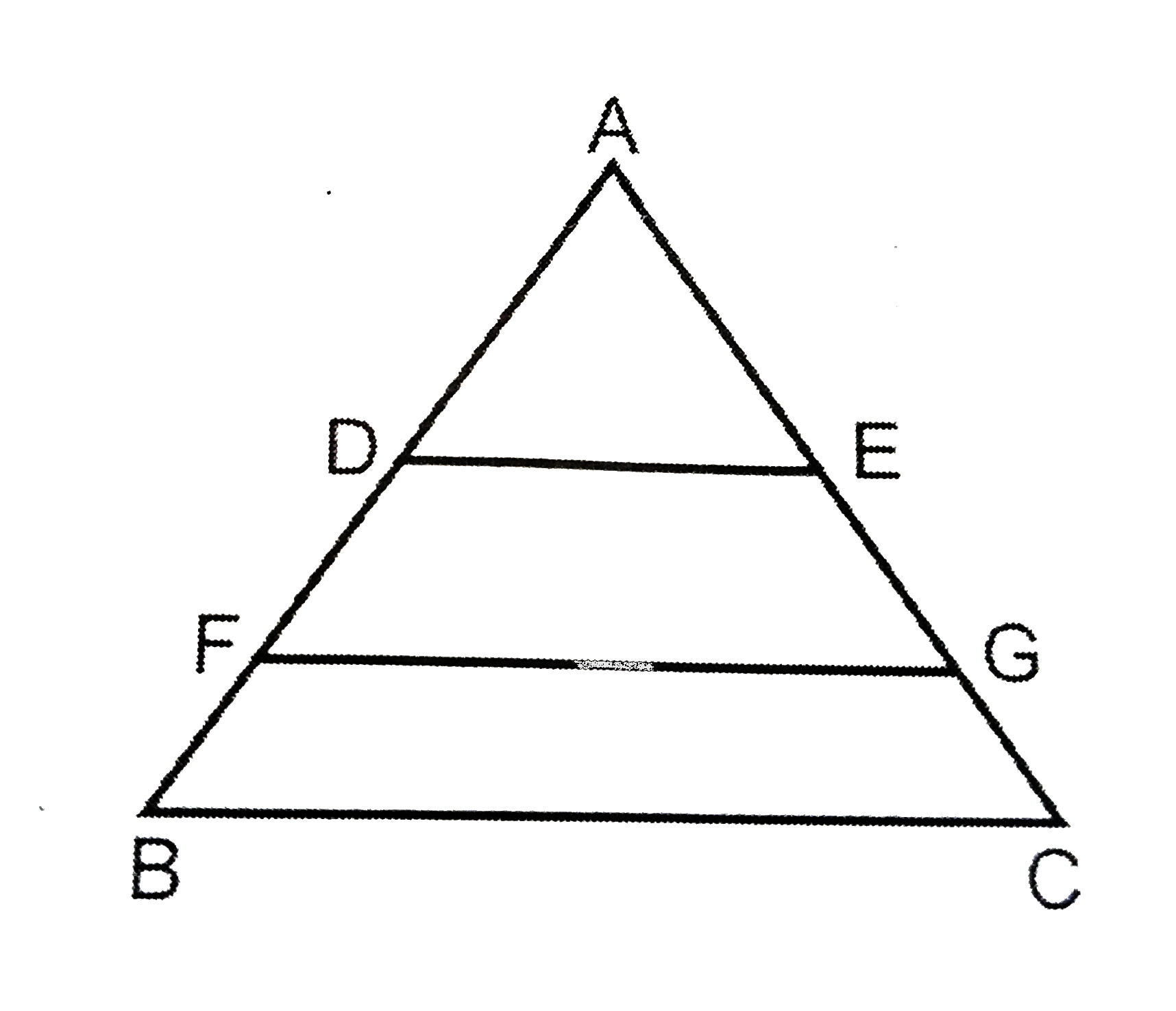
In ΔABC,D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC, If BC=12,what is the length of FG?View SolutionIn the adjoining figure
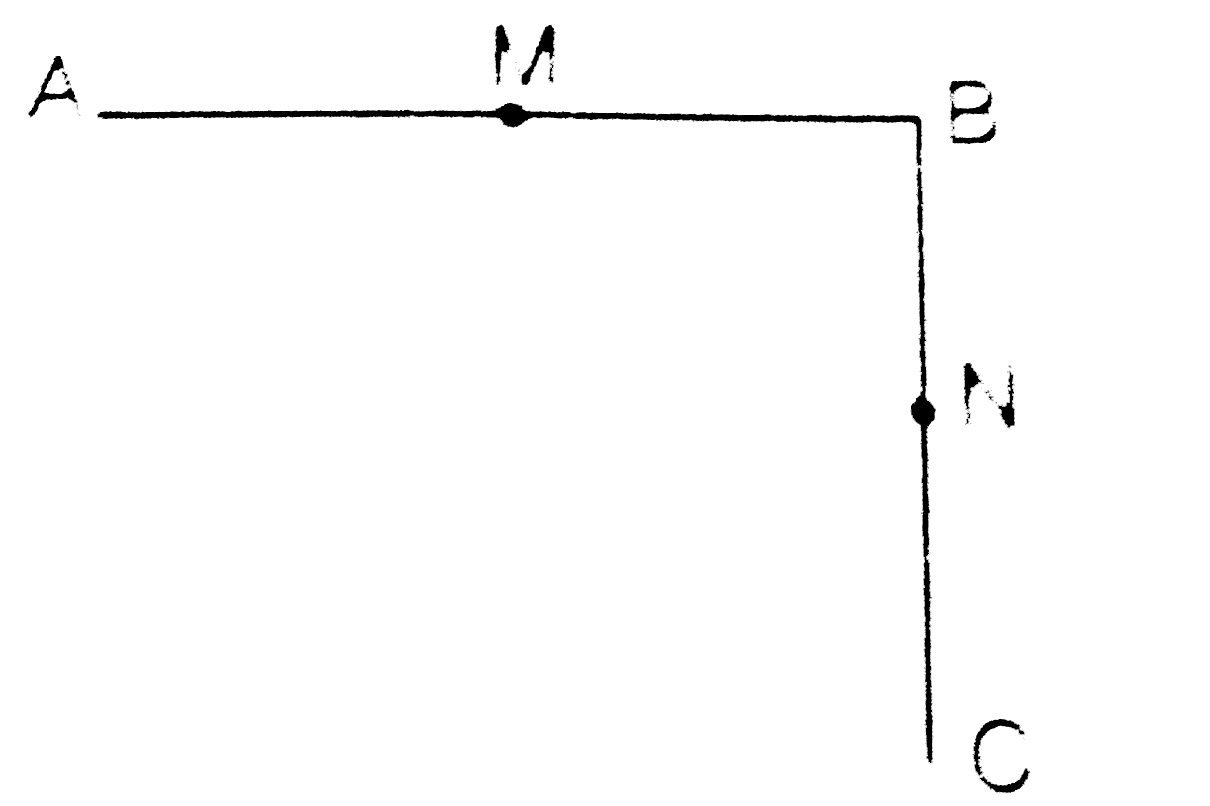
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.View Solution


