ABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2
Calculate
The ratio of PA : DC.
The correct Answer is:1:3
To solve the problem, we need to find the ratio of PA to DC in the parallelogram ABCD given that AP:PB=1:2.
1. Define the segments:
Let AP=x and PB=2x. This is based on the given ratio AP:PB=1:2.
2. Calculate the length of AB:
Since AB=AP+PB, we can write:
AB=x+2x=3x
3. Use properties of parallelograms:
In a parallelogram, opposite sides are equal. Therefore, we have:
DC=AB
Thus,
DC=3x
4. Find the ratio PA:DC:
We know PA=AP=x and DC=3x. Therefore, the ratio can be expressed as:
PADC=x3x
5. Simplify the ratio:
Simplifying the fraction gives:
PADC=13
6. Express in ratio form:
Thus, the ratio of PA:DC is:
PA:DC=1:3
Final Answer:
The ratio of PA:DC is 1:3.
Let AP=x and PB=2x. This is based on the given ratio AP:PB=1:2.
Since AB=AP+PB, we can write:
AB=x+2x=3x
In a parallelogram, opposite sides are equal. Therefore, we have:
DC=AB
Thus,
DC=3x
We know PA=AP=x and DC=3x. Therefore, the ratio can be expressed as:
PADC=x3x
Simplifying the fraction gives:
PADC=13
Thus, the ratio of PA:DC is:
PA:DC=1:3
The ratio of PA:DC is 1:3.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Circle
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Statistics
Explore 9 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Rectillinear figures
Explore 24 Videos
- CHAPTER REVISION (STAGE 2) Book:ICSEChapter:CHAPTER REVISION (STAGE 2) Exercise:DISTANCE FORMULA
Explore 12 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:DISTANCE FORMULA
Explore 11 Videos
Similar Questions
ABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2
Calculate
The area of ΔAPD
View SolutionThe given figure shows a parallelogram ABCD with area 324sq. cm. P is a point in AB such that AP:PB= 1:2. Find the area of ΔAPD.
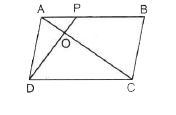
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2
Calculate :
area of parallelogram ABCD.
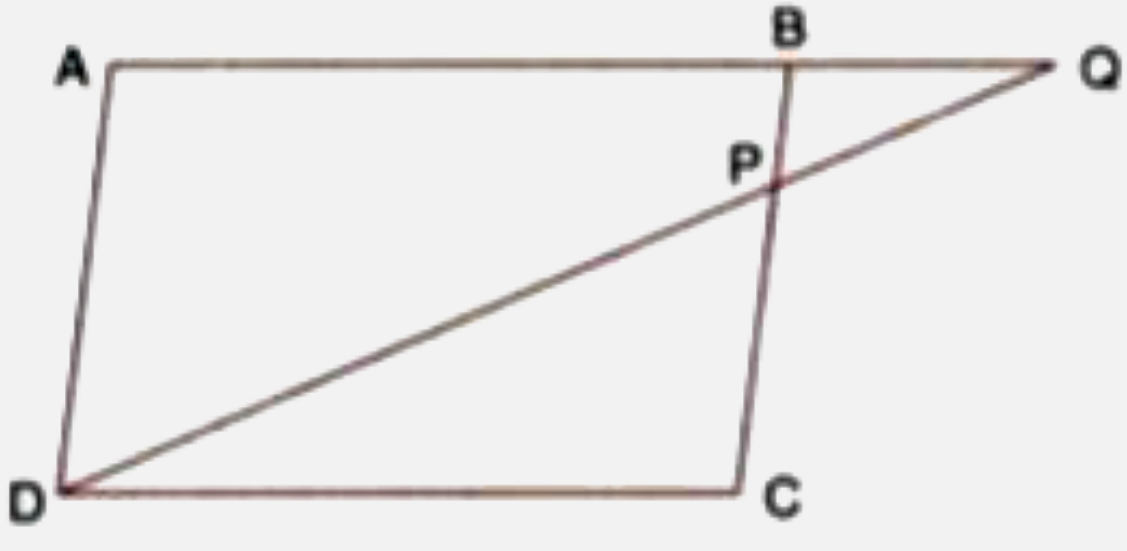
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2

Calculate :
area of triangle CDP.
View SolutionABCD is a parallelogram. If AB = 2AD and P is the mid-point of CD, prove that ∠APB=90∘
View SolutionIn the given figure, P is a point on AB such that AP:PB=4:3. PQ is parallel to AC.
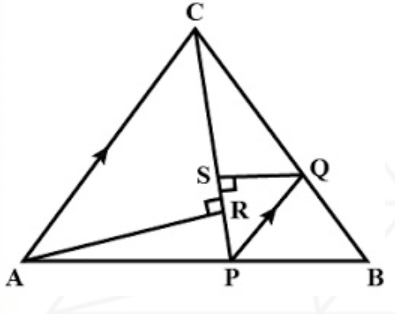
Calculate the ratio PQ : AC, giving reason for your answer.
View SolutionA transversal cuts side AB and AD and diagonal AC of parallelogram ABCD in points P,Q and R respectively such that AP: PB =1 :2 and AQ: QD=2:3 . Find the ratio AR : RC
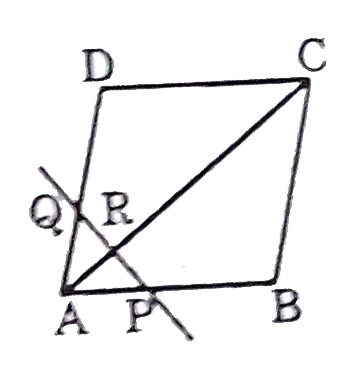
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2EA and F is a point on DC such that DF=2 FC. Prove that AECF is a parallelogram whose area is one third area of parallelogram ABCD.
View SolutionABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
View SolutionIn a parallelogram ABCD, P is a point on side AD such that 3AP = AD and Q is a point on BC such that 3CQ = BC. Prove that : AQCP is a parallelogram.
View Solution

