ABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
To solve the problem, we need to analyze the given information about the parallelogram ABCD and the midpoint X of side AB. We are given that the area of the parallelogram AXCD is 24 cm², and we need to determine if the area of triangle ABC is also 24 cm².
1. Identify the Areas:
- The area of the parallelogram AXCD is given as 24 cm².
- We denote the area of parallelogram ABCD as AABCD.
2. Understanding the Parallelogram:
- In a parallelogram, the diagonal divides it into two triangles of equal area. Therefore, if we denote the area of triangle ACD as AACD and the area of triangle ABC as AABC, we have:
AABCD=AABC+AACD
3. Using the Midpoint:
- Since X is the midpoint of AB, the line segment XC acts as a median for triangle ABC. A median divides a triangle into two smaller triangles of equal area.
- Therefore, we can express the area of triangle ABC as:
AABC=AAXC+ABXC
- Since X is the midpoint, AAXC=ABXC.
4. Relating Areas:
- The area of triangle AXC is half of the area of triangle ABC:
AAXC=12AABC
5. Finding the Area of Triangle ACD:
- The area of triangle ACD can be expressed in terms of the area of the parallelogram:
AACD=12AABCD
- Since AABCD=2×AAXCD (because AXCD and BXC are equal), we have:
AACD=12×24=12 cm2
6. Calculating Area of Triangle ABC:
- Now, we can substitute back into our equation for the area of the parallelogram:
AABCD=AABC+AACD
- We know that AACD=12 cm2, so:
AABCD=AABC+12
- Since AAXCD=24 cm2 and AABCD=2×24=48 cm2:
48=AABC+12
- Solving for AABC:
AABC=48−12=36 cm2
7. Conclusion:
- Therefore, the area of triangle ABC is 36 cm², not 24 cm².
Final Answer:
The statement is False. The area of triangle ABC is 36 cm².
- The area of the parallelogram AXCD is given as 24 cm².
- We denote the area of parallelogram ABCD as AABCD.
- In a parallelogram, the diagonal divides it into two triangles of equal area. Therefore, if we denote the area of triangle ACD as AACD and the area of triangle ABC as AABC, we have:
AABCD=AABC+AACD
- Since X is the midpoint of AB, the line segment XC acts as a median for triangle ABC. A median divides a triangle into two smaller triangles of equal area.
- Therefore, we can express the area of triangle ABC as:
AABC=AAXC+ABXC
- Since X is the midpoint, AAXC=ABXC.
- The area of triangle AXC is half of the area of triangle ABC:
AAXC=12AABC
- The area of triangle ACD can be expressed in terms of the area of the parallelogram:
AACD=12AABCD
- Since AABCD=2×AAXCD (because AXCD and BXC are equal), we have:
AACD=12×24=12 cm2
- Now, we can substitute back into our equation for the area of the parallelogram:
AABCD=AABC+AACD
- We know that AACD=12 cm2, so:
AABCD=AABC+12
- Since AAXCD=24 cm2 and AABCD=2×24=48 cm2:
48=AABC+12
- Solving for AABC:
AABC=48−12=36 cm2
- Therefore, the area of triangle ABC is 36 cm², not 24 cm².
The statement is False. The area of triangle ABC is 36 cm².
Topper's Solved these Questions
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLAR ENGLISHChapter:Areas of Parallelograms and TrianglesExercise:Exercise-9.3 Short Answer Type Questions
Explore 9 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLAR ENGLISHChapter:Areas of Parallelograms and TrianglesExercise:Exercise-9.4 Long Answer Type Questions
Explore 10 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLAR ENGLISHChapter:Areas of Parallelograms and TrianglesExercise:Exercise-9.4 Long Answer Type Questions
Explore 10 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.4
Explore 14 Videos
Similar Questions
ABCD is a parallelogram. If AB = 2AD and P is the mid-point of CD, prove that ∠APB=90∘
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionIn ∠ABC,P is mid-point of median AD.If ar(∠BPD)= 100cm2 then find ar (∠ADC) (in cm2 )
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
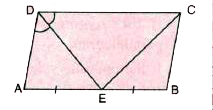
CE bisects angle C
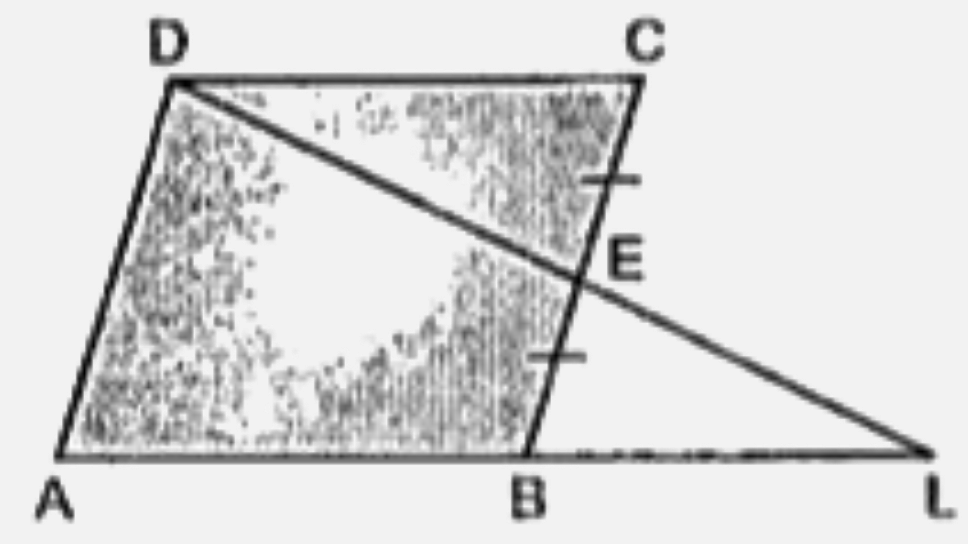
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
AB=BL
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

∠DEC=90∘
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2
Calculate
The area of ΔAPD
View Solution