ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
To solve the problem, we need to show that the area of triangle BDE is equal to one-fourth of the area of triangle ABC, given that D is the midpoint of side BC in the equilateral triangle ABC.
1. Identify the triangles: We have two equilateral triangles, ABC and BDE, with D as the midpoint of side BC.
2. Assign lengths: Let the side length of triangle ABC be denoted as s. Since ABC is equilateral, all sides are equal, so AB=BC=CA=s.
3. Calculate the area of triangle ABC: The formula for the area of an equilateral triangle is given by:
Area=√34×side2
Therefore, the area of triangle ABC is:
AreaABC=√34s2
4. Determine the length of BD: Since D is the midpoint of BC, we have:
BD=DC=BC2=s2
5. Calculate the area of triangle BDE: Since triangle BDE is also equilateral, we can use the same area formula. The side length of triangle BDE is BD, which we found to be s2. Thus, the area of triangle BDE is:
AreaBDE=√34(s2)2
Simplifying this, we get:
AreaBDE=√34×s24=√316s2
6. Relate the areas: Now, we can relate the area of triangle BDE to the area of triangle ABC:
AreaBDE=√316s2
We can express the area of triangle ABC in terms of the area of triangle BDE:
AreaABC=√34s2
To find the relationship:
AreaBDE=14AreaABC
7. Conclusion: Thus, we have shown that:
AreaBDE=14AreaABC
This completes the proof.
Area=√34×side2
Therefore, the area of triangle ABC is:
AreaABC=√34s2
BD=DC=BC2=s2
AreaBDE=√34(s2)2
Simplifying this, we get:
AreaBDE=√34×s24=√316s2
AreaBDE=√316s2
We can express the area of triangle ABC in terms of the area of triangle BDE:
AreaABC=√34s2
To find the relationship:
AreaBDE=14AreaABC
AreaBDE=14AreaABC
This completes the proof.
Topper's Solved these Questions
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.3 Short Answer Type Questions
9 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
Similar Questions
ABC and BDE are two equilateral triangles such that D is the mid-point of BC . The ratio of the areas of the triangles ABC and BDE is 2:1 (b) 1:2 (c) 4:1 (d) 1:4
View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
View SolutionTick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2:1 (B) 1:2 (C) 4:1 (D) 1:4
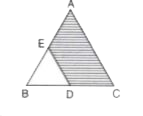
View SolutionABC and BDE are two equilateral triangles such that D is the mid- point of BC. If AB = 20 cm . Find the area of the shaded portions [ Take √3=1.73]
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC in F. Prove that: ar(△BFE)=2ar(△FED).
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).

View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIf sa=4 then area of the equilateral triangle ΔABC is equal to
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionThe given figure shows an equilateral triangles ABC and D is point in AC.
Prove that :
(i) AD<BD
(ii)BC>BD
View Solution
