Which of the wavelengths 4000 A o and 8000 A o has a higher frequency?
To determine which of the two wavelengths, 4000 Å (angstroms) and 8000 Å, has a higher frequency, we can use the relationship between wavelength (λ), frequency (ν), and the speed of light (c). The formula is given by:
c=ν⋅λ
Where:
- c is the speed of light (approximately 3×108 m/s),
- ν is the frequency,
- λ is the wavelength.
1. Identify the Wavelengths:
- Wavelength 1 (λ₁) = 4000 Å
- Wavelength 2 (λ₂) = 8000 Å
2. Convert Wavelengths to Meters:
- Since 1 Å = 1×10−10 m,
- λ₁ = 4000 Å = 4000×10−10 m = 4×10−7 m
- λ₂ = 8000 Å = 8000×10−10 m = 8×10−7 m
3. Use the Formula for Frequency:
- Rearranging the formula c=ν⋅λ gives us:
ν=cλ
4. Calculate the Frequency for Each Wavelength:
- For λ₁ (4000 Å):
ν₁=3×108 m/s4×10−7 m
ν₁=7.5×1014 Hz
- For λ₂ (8000 Å):
ν₂=3×108 m/s8×10−7 m
ν₂=3.75×1014 Hz
5. Compare the Frequencies:
- ν₁ (for 4000 Å) = 7.5×1014 Hz
- ν₂ (for 8000 Å) = 3.75×1014 Hz
6. Conclusion:
- Since ν₁>ν₂, the wavelength of 4000 Å has a higher frequency than the wavelength of 8000 Å.
Final Answer:
The wavelength of 4000 Å has a higher frequency than the wavelength of 8000 Å.
---
- c is the speed of light (approximately 3×108 m/s),
- ν is the frequency,
- λ is the wavelength.
- Wavelength 1 (λ₁) = 4000 Å
- Wavelength 2 (λ₂) = 8000 Å
- Since 1 Å = 1×10−10 m,
- λ₁ = 4000 Å = 4000×10−10 m = 4×10−7 m
- λ₂ = 8000 Å = 8000×10−10 m = 8×10−7 m
- Rearranging the formula c=ν⋅λ gives us:
ν=cλ
- For λ₁ (4000 Å):
ν₁=3×108 m/s4×10−7 m
ν₁=7.5×1014 Hz
ν₂=3×108 m/s8×10−7 m
ν₂=3.75×1014 Hz
- ν₁ (for 4000 Å) = 7.5×1014 Hz
- ν₂ (for 8000 Å) = 3.75×1014 Hz
- Since ν₁>ν₂, the wavelength of 4000 Å has a higher frequency than the wavelength of 8000 Å.
The wavelength of 4000 Å has a higher frequency than the wavelength of 8000 Å.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following has longest C-O bond?
A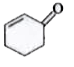 B
B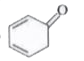 C
C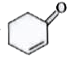 D
D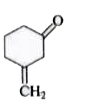
(a) Write the approximate wavelength for (i) blue, and (ii) red light
(b) The wavelength of violet and red light are 4000Å and 8000Å respectively. Which of the two has higher frequency?
View SolutionTwo black bodies A and B emit radiations with peak intensities at wavelengths 4000 A and 8000 A respectively. Compare the total energy emitted per unit area per second by the two bodies.
View SolutionWhy is the ratio of the velocities of light of wavelengths 4000 Å and 8000 Å in vacuum 1 : 1?
View Solution(a) Compare the speed of light of wavelength 4000 Å (i.e., violet light) and 8000 Å (i.e. red light) in vacuum.
(b) How is the refractive index of a medium related to the speed of light in it and in vacuum or air ?
View SolutionThe relationship between energy (E) of wavelength 2000A0and8000A0 , respectively is
View SolutionFind the ratio of frequencies of light waves of wavelengths 4000 A and 8000 A.
View SolutionWhich has a higher energy, a photon of violet light with wavelength 4000 A ˚ or a photon of red light with wavelength 7000 A ˚ ?
View Solution
