Consider Example 8, taking the coefficient of friction, μ, to be 0.5 and calculate the maximm compression of the spring.
Both the frictional force and the spring force act so to oppose the compression of the spring as shown in figure.
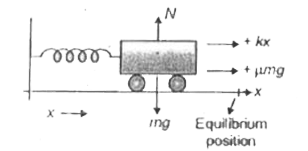
Use the work - energy theorem,
The change in KE=ΔK=Kf−Ki=0−12mv2
The work done by the net force is W=−12Kx2m−μmgxm
Equating the two, we get
12mv2=12Kx2m+μmgxm
μmg=0.4×1500×10=6000N
Kx2m+2μmgxm−mv2=0 (After rearranging the given equation)
xm=−2μmg+√4μ2m2g2−4(k)(−mv2)2K (Taking +ve sign with square root as xm is +ve)
=−μmg+√μ2m2g2−4(k)(−mv2)K
=−0.4×1500×10+√(0.4×1500×10)2+1500×7.5×103×1027.5×103
=3.75m
Which, as expected, is less than the result in Example 14. If the two forces on the body consist of a conservative force Fc and a non - conservative force Fnc the conservation of mechanical energy formula will have to be modified. By the W-E theorem.
(Fc+Fnc)Δx=ΔK
But FcΔx=−ΔV
Hence, Δ(K+V)=FncΔX
ΔE=FncΔx
where E is the total mechanical energy. Over the path this assumes the form
Ef−Ei=Wnc
where Wnc is the total work done by the non - conservative forces over the path Unlike conservative force Wnc depends on the path taken.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:IILUSTRATION
Explore 2 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
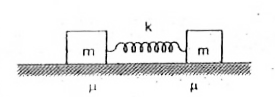
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
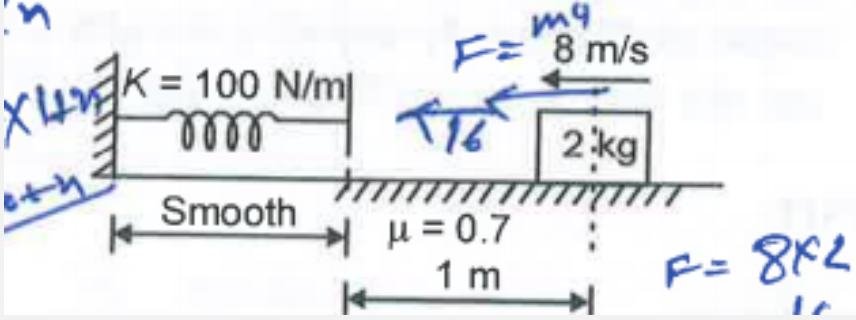
View SolutionFree end of an ideal spring of spring constant 100 N/m is at a distance 1 m from a vertical block of mass 2 kg moving on rough surface with initial speed 8 m/s as shown in figure. If coefficient of friction is 0.7, then maximum compression in spring is (g=10ms−2)
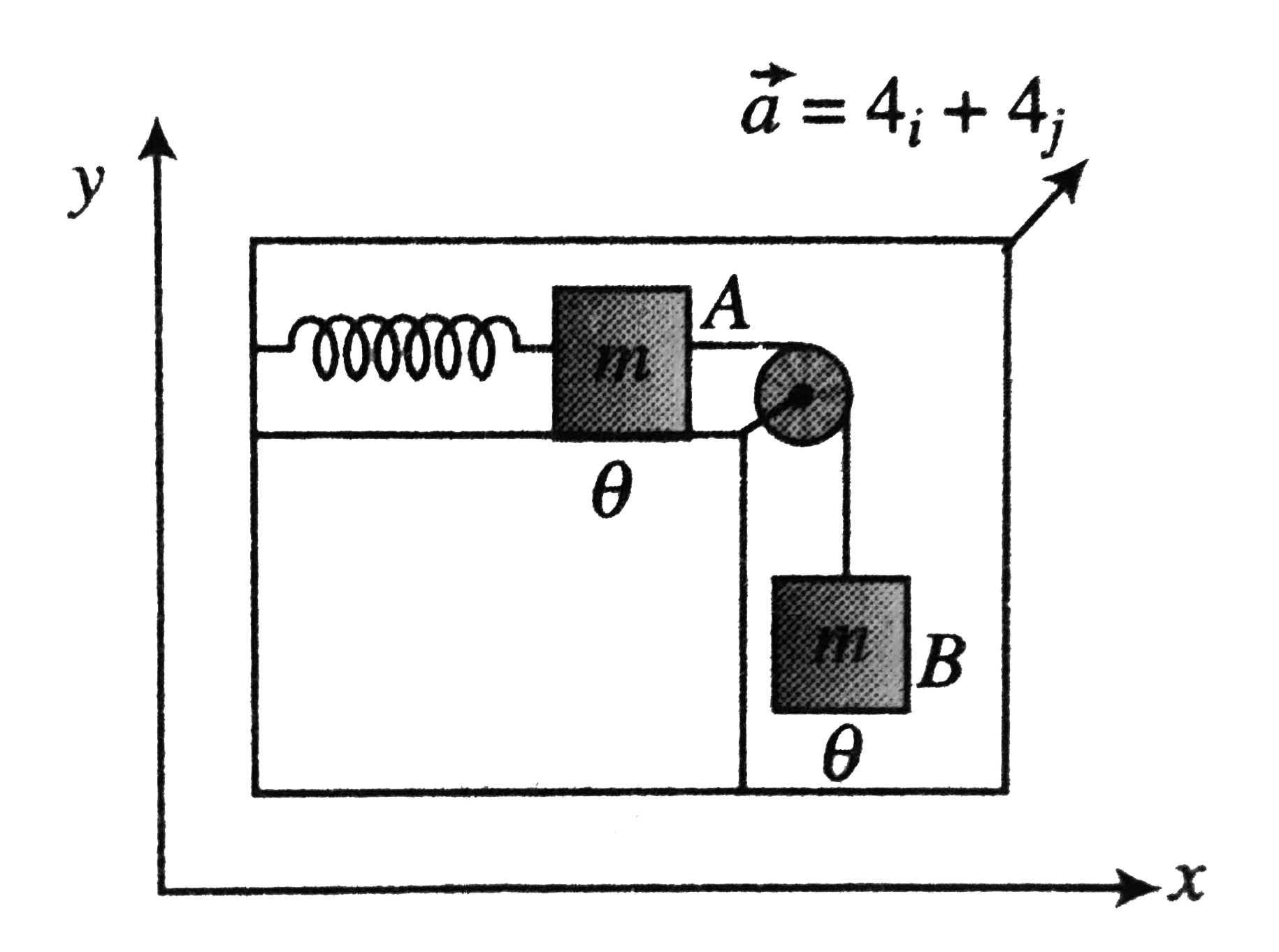
View SolutionThe arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a friction less pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in 10(m) of the spring. (g=10ms−2).
View SolutionThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
View SolutionA force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
View Solution
Consider the figure shown here of a moving cart C. if the coefficient of friction between the block A and the cart is μ, then calculate the minimum acceleration a of the cart C so that the block A does not fall.
View Solution .
.
In the figure shown, AB=BC=2m. Friction coefficient everywhere is μ=0.2. Find the maximum compression of the spring.
View SolutionA car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
View SolutionBlocks A and B in the Fig are connected by a bar of negligible weight .Mass of each block is 170kg and μA=0.2 and μB=0.4 where μA and μBare the coefficient of limiting friction between bloock and plane calculate the force developed in the bar(g=10ms−2)
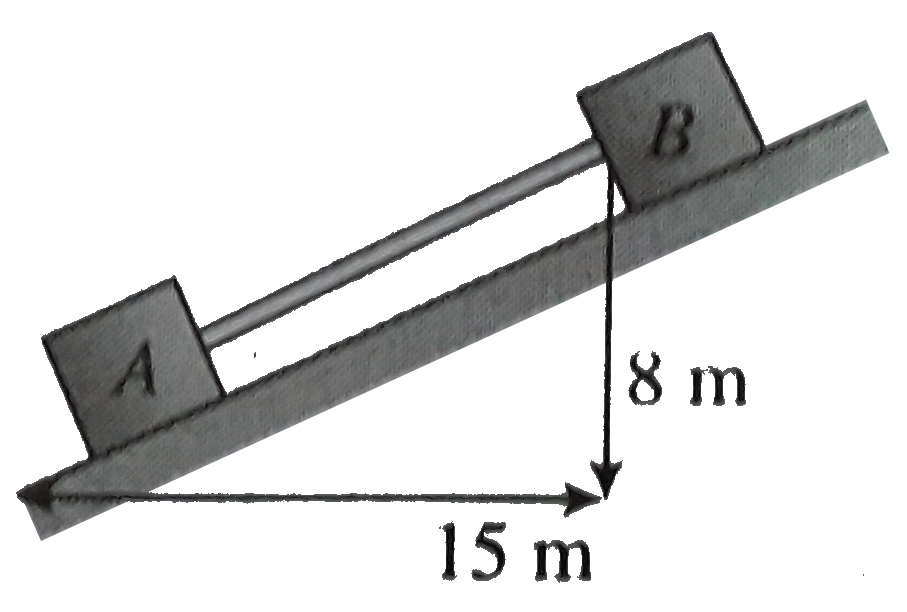
View Solution